1．4．4 ART模型的学习算法
ART模型是一种有自组织能力的神经网络模型，它是通过竞争机制在F2中建立对应于输入模式I的编码的。
在F2中形成对应于输人模式I的编码；在本质上就是对外界输入模式I进行学习，使网络的权系数取得恰当的对应值。这就要按照一定的规则或者学习算法来对权系数进行修改。
下面分别就F1到F2，F2到F1的权系数学习过程进行介绍。
一、自下而上的权系数学习算法
所谓自下而上，也即是从F1到F2的方向；自下而上的权系数就是从F1到F2的权系数。F1中的神经元用Ni表示，F2中的神经元用Nj表示；则从F1的神经元Ni到F2的神经元Nj的权系数用wij表示。
在学习时，权系数Wij用下面的方程来修正：
 |
(1-63) |
其中：f(xj)是神经元Nj到F1的输出信号；
h(Xi)是神经元Ni到F2的输出信号；
Eij是参数；
K1是参数。
对于参数Eij，一般按下式选取
 |
(1-64) |
其中：L为常数L-1＝1/L。
如果取K1为常数，并且有K1＝KL，则权系数Wij的微分方程可以写成
这个方程说明：当F2层中神经元Nj的输出为正时，来自F1层中神经元Ni正的输出信号以速率(1-Wij)Lh(Xi)Kf(Xj)来影响权系数Wij的改变。
在上面方程中，
所有输入神经元中i≠k的输出信号h(Xk)的总和；这个信号也就是F1中除Ni以外的其它所有神经元对F2中神经元Nj的输人信号。ART模型就根据这个信号的大小来增强与Nj相对应的连接权系数。
二、自上而下的权系数的学习算法
从F2到F1的权系数称为自上而下的权系数，它用Wji表示。权系数Wji满足如下方程：
 |
(1-65) |
其中：f(xj)是神经元Nj到F1的输出信号；
h(Xi)是神经元Ni到F2的输出信号；
K2，Eji是参数，一般简单取K2＝Eji-1
很明显，Wji的微分方程可以写成下式：
如果从F2来的学习期望和外部输入在F1中不能匹配时；调整子系统A就会产生一个重置信导到F2中去，改变F2的状态，取消原来的学习期望输出。显然，在这时取向子系统处于工作状态。输入模式为I，它是一个n维向量，故有n个元素。当I输人到ART网络的F1层时，它就会送m个大小固定为P的信号到A中。这样，从输入端到A的所有激励信号为n’P。同样，F1中的神经元也同时产生一个大小固定为Q的抑制信号送到A中；F1中的激活模式为X，而对应于激活模式X从F1到A的激话连接个数为I；那么，从F1到A的所有的抑制信号为IQ。如存在条件
n'p>IQ
则说明激励作用大于抑制作用．则取向子系统A就会收到激励信号，并产生一个重置信号到F2中，令
 |
(1-67) |
并称为取向子系统的警戒线参数。
考虑在n'P>IQ时有
 |
(1-68) |
| 显然有 | |
 |
(1-69) |
这时，则A会产生重置信号到F2。反亦反之。
当A把重置信号送到F2时，F2中的神经元的输出按下式进行修正：
 |
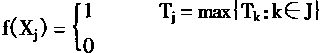(1-70) |
其中：Tj是从F1来的到F2的输入模式；
J是F2中神经元的一些集合；这些神经元在学习过程中末被置以新值。
在学习的过程中，每个学习周期开始把J置为(n+1，n+2，……m)。随着学习过程的继续，在这个周期内每次递归都应从J中清去一个F2神经元的下标．直到产生了正确的匹配才停止。
自适应共振理论模型ART的数学分析以及学习算法有关情况可以用图1—26所示的框图表示。
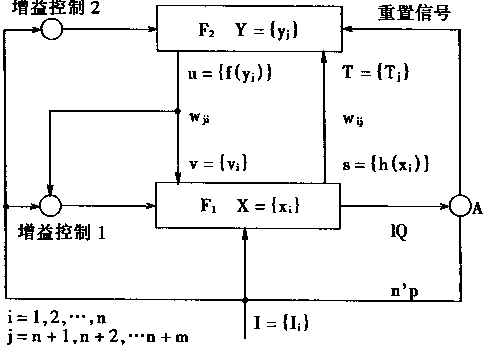
图1-26 数学分析及算法有关图示
1．4．5 ART模型的Lippman学习算法
ART网络有多种学习算法，在这部分介绍Lippman在1987年提出的算法。这个算法的步骤及执行过程如下：
一、初始化
初始化时对从F1到F2的权系数Wij，F2到F1的权系数Wji以及警戒值P进行初设定。
1．F1到F2的权系数wij初始化
Wij的初始值按下式设定：
 |
(1-71) |
其中：n为输入向量I的元素个数；
L为大于1的常数，一般取L＝2。
为了方便，可直接取：
 |
(1-72) |
Wij(0)的值不能太大，太大则网络可能把识别层F2的所有神经元都分配给一个输入模式。
2．F2到F1的权系数Wij初始化
Wji的初始值取为1，即有
Wji(0)=1 (1-73)
Wji(0)的值不能太小，太小则导致比较层F1不匹配。
3．警戒值P的初始化
P的值按下列范围选取：
0≤P≤1 (1-74)
P的值的选择要恰当。P的值太大，则网络会过细辩别差异iP的值太小，则容易把稍有某点相似的输入模式都当作同一类。在学习中，一开始取小的P值，进行粗分类；然后，逐渐增大警戒值P，进行逐步细分类。
二、输入一个新的模式
三、进行匹配度计算
由于识别层是输入向量I的分类器，为了考虑输入向量I和识别层中对应的神经元相关的权系数形态是否匹配，故而要求其匹配程度。这时，计算识别层每个神经元j的激活量Yj。
 |
(1-75) |
其中：Yj为识别层神经元j的激活值；
Si为比较层神经元i的输出；
k是学习的次数。
四、选择最优匹配神经元C
ART网络在识别层通过横向抑制，从而使到只有激活值最大的神经元c才能输出1，其它神经元则输出0。神经元C的激活值用Yc表示，则：
 |
(1-76) |
| 考虑识别层的神经元传递函数f为阶跃型函数，即有输出Uj | |
 |
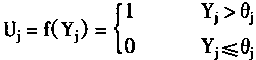(1-77) |
其中：Yj是神经元j的激活值；
θj是神经元j的阀值；
Uj是神经元j的输出。
五、比较和试验警戒值
识别层的神经元在选择出最优匹配的神经元之后，则有1输出，故而比较层增益控制输出0。依据2／3规则，比较层中U和I的元素均为1的神经元被激活。取向子系统A则对比较层输出的向量s和输入向量I进行比较，如果相似率低于警戒值P，则向识别层发出重置信号，对识别层进行清零。向量S和向量I的相似率用R表示，则有
 |
(1-78) |
其中：‖S‖是s向量的元素值之和，‖s‖＝ΣSi；
‖I‖是I向量的元素值之和，‖I‖=ΣIi
在上面‖S‖和‖I‖的实际计算方法如下：
S＝101O1011 ‖S‖＝5
I=11111001 ‖II‖=6
由于比较层输出s是由输入向量I和识别层输出向量U共同作用产生的；同时，因神经元c的输出为1，向量U在本质上是等于取得最优匹配的神经元c从F2到F1的权系数向量Wci。
按2/3规则，两个输入同时为1时输出才能为1。则向量s的元素si；可表示为：
Si=Wci.Ii (1-79)
故而
 |
(1-80) |
如果相似率R大于警值P，即有
R>P
则转向第七点执行，否则继续向下执行第六点。
六、最优匹配无效及其处理
如果相似率R小于警戒值p，即R<P，所以，应对其余存储的模式进行搜索，以便找到一个和输入模式更加接近的存储模式。
这时，重置信号到识别层去对神经元清0，则原来选中的最优匹配神经元为0，也说明取消了该神经元的优胜性；把比较层增益控制设置为输出1，转到第三点，重复上面过程。
在识别层一个神经元所取得的相似率大于警似值，则转向策七点，结束分类过程。
在识别层的全部神经元都被搜索过，但没有一个神经元能匹配，则经学习后确定识别层—个神经元作为输入模式的最优匹配单元；然后停止分类学习过程；则输入模式被存储。分类过程结束时，则从F2到F1的权系数全部为1；比较层输出S等于I，相似率等于1。
七、自学习过程
自学习时，给出一组模式样本向量，按一定顺序作为网络的输入向量，对ART网络的权系数进行调整．使相似类向量都激活识别层同一神经元。
自学习算法如下：
1．计算F1到F2的权系数Wij
计算公式如下：
 |
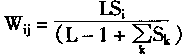(1-81) |
其中：Si是比较层输出向量S的第i个元素；
j是识别和最优匹配神经元序号；
Wij是比较层神经元i与识别层神经元j之间的权系数
L是大于1的常数。
2．计算F2到F1的权系数Wji
把Wji调整为等于向量S中相应元素的二进制值：
Wji=Si (1-82)
在实际求Wij和Wji时，可以采用下面的有效式子。
 |
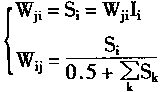(1-83) |
| 考虑到学习次数k，则上面式子写成 | |
 |
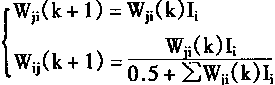(1-84) |
用其它向量对网络继续进行学习时，则会把这些向量中元素值为0的对应权系数置0。这样．一组向量全部学习完毕时，则这组向量的元素中有多少个0，则相应位置中的权系数都被置0。学习之后所存储的权系数形态，是全组向量的“交”形式。这时的权系数形态也是全组向量基本特征。显然，这等于抽取插入模式的特征。
3．比较层输出S中1的个数越多，则从F1到F2的权系数Wij越小。
从F1到F2的权系数调整公式为：
 |
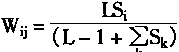(1-85) |
在分母中，ΣSk是比较层输出S中1的个数，它表示了向量S的“大小”。显然，ΣSk越大则Wij越小。也就是比较层输出S的“大小”对权系数Wij有自动调节作用。
这是一个重要特点，它可以判别两个输入向量中，其中一个是否是另一个的子集。ART网络在自学习过程结束之后，则自动返回第二点；从而准备开始对输入的新模式进行分类。
在上面Lippman学习算法中可以看出有如下一些特点：
1．F2到F1t的权系数Wij(0)必须初始值取1。
因为．比较层的输出s是由输入向量I和最优匹配神经元的权系数Wji；按2/3规则产生。只有I和Wji都为1，s的元素才会为1。
如果Wji(0)＝0，则S的元素会全部为0。则无法进行模式识别。
实际上，搜索过程是一个“剪裁”与输入向量不匹配的存储模式元素的过程，这是一个不可逆的过程；一旦权系数取值为0，那么，学习算法是无法使其再取非零的值的。
2．抽取输入模式的特征
对于一组相似的向量，会被ART网络中识别层F2中的一个神经元识别为同一类。
在用这组相似的向量对网络执行学习时，第一个向量学习的结果选中F2中的一个神经元。