2.2 神经网络控制器与学习
在神经网络控制系统中,有时需要对对象进行仿真;所以,在系统中设置有神经对象仿真器NPE(Neural Plant Emulator);同时,在系统中还有神经控制器NC(Neural Controller)。不论对象仿真器PC,还是神经控制器NC,都需要学习;而对于控制系统中,联机学习是最重要的。在这一节中,介绍对象仿真器,神经控制器,学习训练的结构,联机学习方法及算法。
2.2.1 对象仿真器及神经控制器
在控制中,大量采用多层前向神经网络。多层神经网络MNN(Multilayer Neural Network)可以认为是一个有映射学习能力的结构。基于映射能力,得到两种通用的神经控制结构:即对象仿真器PE和神经控制器NC。
对于一个单输人单输出的过程,从数字控制技术可知有如下离散数学模型:
y(k+1)=f[y(k),y(k-1),......,y(k-P+1),u(k),u(k-1),......,u(k-Q)] (2.15)
其中:y是输出,u是输入,k是离散时间系数,P,Q是正整数.f[·]是函数。
在很多情况中,对象的输入信号u是在幅度上范围有限的;既存在下限um和上限uM对于任何k,有
um≤u(k)≤uM (2.16)
在描述对象的式(2.15)中,对应P,Q的估计值分别用P,q表示。
一、对象仿真器PE
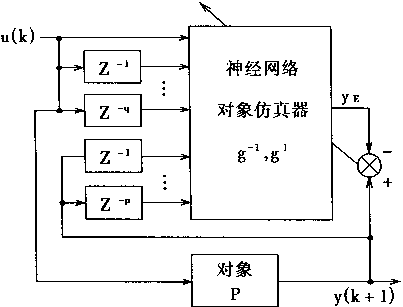
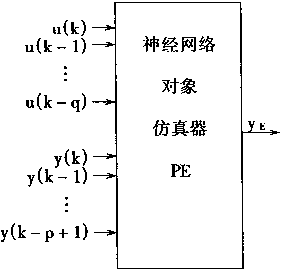
对象仿真器PE的作用和意义如图2—7所示。其中,图2—7(a)表示PE在按制系统和对象之间的关系;图2—7(b)表示PE的框图。在图中u(k)Z-1和u(k-1)是一样的.z-1是延时算子,其意义是延时一拍,即延时一个采样周期。
从图中看出,用多层神经网络MNN组成的PE有p+q+1=m个输入,一个输出。它可以用于对式(2.15)描述的对象进行仿真。PE的映射功用ΨE(.)表示,输出用yE表示当输入为m维向量XE(k),且
XE(k)=[y(k),......,y(k-p+1),u(k),......,u(k-q)]T (2.17)
则仿真器PE有输出
yE=ΨE(XE) (2.18)
对仿真器进行训练,应使仿真误差eE
eE=y(k+1)-yE
达到最小。
(a) |
(b) |
图2-7 对象仿真器PE
二、神经控制器NC
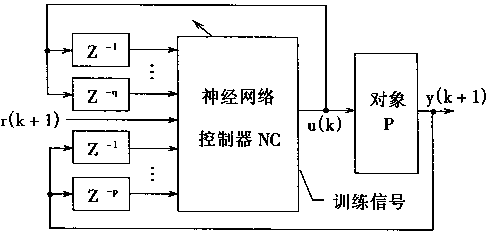
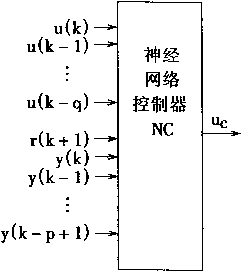
神经控制器NC的作用和意义如图2-8所示。图2-8(a)是NC在系统中的位置,图2-8(b)是NC框图。
假定由式(2.15)所描述的过程对象是可逆的,则会存在函数g[·],并且有
u(k)=g[y(k+1),y(k),......,y(k-p+1),u(k-1),u(k-2),......,u(k-Q)] (2.19)
以神经网络可实现式(2.19)所描述的对象逆模型。并且,输入为m维向量Xc,输出为Uc,则输出输入关系表示为
Uc=ψc(Xc) (2.20)
其中:ψc为输入输出映射。
如果ψc(·)的输出逼近g(·)的输出.则逆模型的神经网络可以看作是控制器。在k时刻,假设输入xc(k)为
Xc(k)=[r(k+1),y(k),......,y(k-p+1),u(k-1)...,u(k-q)]T (2.21)
在上式(2.21)中,以给定输入r(k+1)取代未知的y(k+1);p和q分别是P和Q的估计值。
根据式(2.20),则神经网络控制器NC有输出
uc(k)=ψc[r(k+1),y(k),...,y(k-p+1),u(k-1),...,u(k-q)] (2.22)
在神经网络控制器NC的训练结果足以使输出偏差e(k)=r(k)-y(k)保持为一个很小的值时.则有
Xc(k)=[r(k+1),r(k),...,r(k-p+1),u(k-1),...,u(k-q)]T (2.23)
在上式中,是以r(t)取代y(t);这个式子明显突出了神经网络控制NC的前馈特性。
(a) |
(b) |
图2-8 神经控制器NC
2.2.2学习训练的结构
在神经网络控制器的训练中,一般要求对象输出的偏差e(k)=r(k)—y(k)所定义的偏差函数J最小化。为了能采用梯度法进行学习,同时还需考虑J对NC输出的微分,即δ=—3J/Juc。有S之后,通过BP算法就可以改善NC的权系数。在这种基础上,考虑直接逆控制,直接适应控制和间接适应控制的训陈结构。直接逆控制中的神经网络控制器NC是对象的逆模型。因此,可以通过图2-9所示的结构训练逆模型。
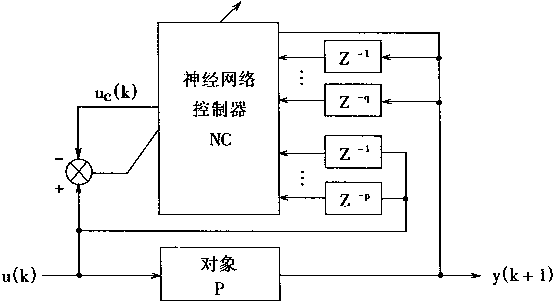
图2-9 直接逆控制训练结构
在K+1时刻,设神经网络控制器NC的学习输入为Xc*(k)
Xc*(k)=[y(k+1),y(k),...,y(k-p+1),u(k-1),...,u(k-q)]T (2.24)
则神经网络控制器NC有输出Uc(k)
uc(k)=ψc[Xc*(k)] (2.25)
即有
uc(k)=ψc[y(k+1),y(k),...,y(k-p+1),u(k-1),...,u(k-q)] (2.26)
对于NC而言,有训练输出偏差ec
ec(k)=u(k)一uc(k) (2.27)
定义偏差函数J为
J(k)=0.5[ec(k)]2=0.5[u(k)—uc(k)]2 (2.28)
则J对uc的导数为δk
![]() (2.29)
(2.29)
很明显,这种训陈结构用BP算法是十分方便的。
二、直接适应控制训练结构
直接适应控制中,神经网络控制器NC是通过对象的输出偏差e(k)=r(k)-y(k)来实现训练效果判别和训练的执行的。显然,这和逆模型的训练不同。这种训练结构如图2—10所示。
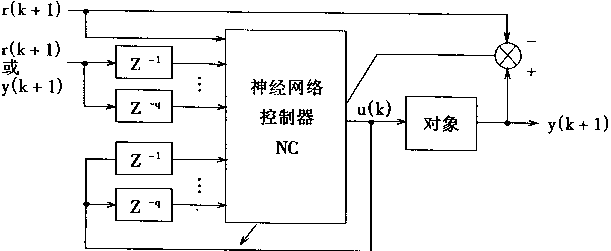
图2-10 直接适应控制训练结构
假定对象的逆模型存在.那么,应有式(2.19)所示的形式。如果逆模型是准确的.那么,以逆模型构成的神经控制器NC对对象的控制总可以使输出偏差e(k)=r(k)—v(k)趋于无穷小。
直接适应控制不是先给出逆模型,而是根据输出的偏差e,去对Nc进行训练.令其逼近于逆模型。在直接适应控制结构中,先期已知的条件有两个:
1.神经网络控制器NC有式(2.19)的结构形式。
2.输出偏差e(k)=r(k)—y(k)
为了进行训练,偏差函数J的格式取
J(k)=0.5[e(k)]2=0.5[r(k)-y(k)]2 (2.30)
由于,NC的输出为u(k),而在训练中需要求取偏差函数J对M的导数,则有3
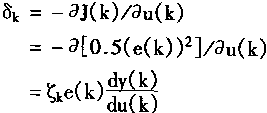 |
(2.31) |
其中:ζk是二进制因子,取1或0,它用于说明对输入u(k)的约束。同时避免错误训练NC而无法跟踪给定输入I。
令
| (2.32) | |
| 对于以式(2.15)、(2.16)描述的系统,在k时刻ζk取值如下 | |
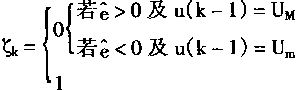 |
(2.33) |
在式(2.31)中加入电等于在Nc输出和对象输入之间存在一个限幅器。当式(2.16)所表示的u(k)产生错误输出而超界时,这时限幅器就会饱和,同时,式(2.31)产生因ζk=0而得到的ζk=0;这时就会禁止学习。而当给定输入r可以被跟随时,则学习正常执行。
三、间接适应控制训练结构
间接适应控制与直接适应控制不同;神经网络控制器的训练的依据是给定信号r和对象仿真器的偏差eE=r(k)—yE(k);而对象仿真器的训练的依据是对象输出y(k)与对象仿真器输出yE(k)的偏差ec=y(k)—yE(k)。间接适应控制训练结构如图2—11所示。
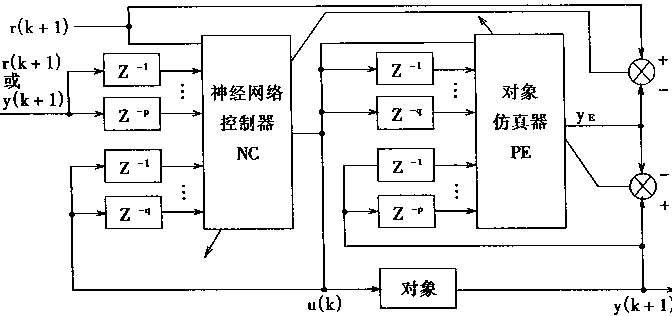
图2-11 间接适应控制训练结构
在训练时,偏差函数J对NC输出u的导数δ=-aJ/au,它的算术符号足以指示出J的梯度方向。
在不少实际情况中,式(2.31)中的导数
![]()
可以容易地用导数的符号,即+1或-1取代;不过,这不带有普遍性。所以,通常需要求导数dy(k)/du(k)的结果;但是,dy(k)/du(k)的结果是相当难求取的。
在间接适应控制中,对象仿真器PE用于计算偏差函数J对NC输出u的导数6。由于PE是一个多层前向网络。采用BP算法可以容易计算出δ。这就克服了dy(k)/du(k)在前述的求取困难的问题。
图2—11所示的结构还有一个特别的优点,这就是当对象的逆模型不能求取时,这种结构特别有用。为了改进控制器的性能,NC和PE可以认为是m维输入单输出的多层神经网络的可变部件和固定部件。对于PE,可以采用对象足够丰富的有关数据进行前期的脱机训练;然后,再把NC、PE进行联机训练。在某种意义上讲,既是执行系统对象辨识的;所以.对于状态变化迅速的系统,考虑到鲁捧性,修改PE的频繁度比修改Nc的频繁度高是合理的。
2.2.3联机学习方法及算法
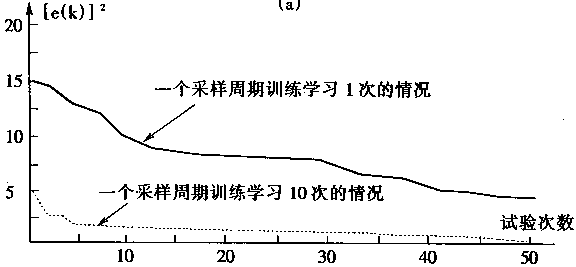
神经网络控制需要良好的控制器,而神经网络控制器的训练收敛速度和时间相当长,这使到在实际控制中执行联机学习几乎不可能。为了使神经网络控制器可以进行实时学习,人们对提高训练收敛速度进行了不少研究。这些研究的主要思想有如下几种:
1.开发有效的BP算法。
2.在多层神经网络结构中,对象结构知识具体化。
3.和控制结构相关的神经网络混合系统。
4.预学习和有效的初始化过程。
在控制系统中,如果提高采样频率,显然,每个采样周期Ts执行一次学习,就会减少学习时间。但是,实际控制系统中,往往对采样周期Ts有一定的要求。比如温度,化学反应控制过程等就要求采样周期Ts较长。同时,高速采样也会要求系统有相应的复杂控制结构;从而使代价提高。
如果在不改变采样频率的条件下提高学习频率;很明显会减少学习时间。这样在联机中学习就成为可能;神经网络控制实时学习就可以实现。
为了实现实时学习,考虑学习周期TL,由于学习周期TL只是由计算机运算时间决定,所以,一般学习周期TL比采样周期Ts要小得多。显然,只要在一个采样周期Ts中执行多次学习周期TL会大大加快学习过程。
一、对象仿真器PE训练学习
假定在k+1时刻对象的输出为y(k+1),而对象先前的p-1+t个输出值存贮在存贮器中,即有y(k),y(k-1),...,y(k-p+1-t)
同时,对象的输人为u(k+1),而先前的q+t个输入值存在存贮器中,即有
u(k),u(k-1),...,u(k-q-t)
很明显可以用XE(k-i),y(k+1-i)数据对对系统的PE进行训练。当取i=0,1,2,...,t-1时,显然有t对XE(k-i),y(k+1-i)。并且注意,这是在采样序号k+1时,也即k+1为定值时对PE执行训练。k+1时刻第i个m维输人学习向量为
XE.i(k-i)=[y(k-i),y(k-1-i),...,y(k-p+1-i),u(k-i),u(k-1-i),...,u(k-q-i)]T (2.34)
则在PE的输出产生输出结果yE(k+1-i)
yE.i(k+1-i)=ψE[XE.i(k-1)] (2.35)
考虑偏差函数JE
![]()
其中:1≥λ0≥λ1≥...≥λt-1是一个权系数序列,它们的作用用于强调最新的数据,减弱旧数据的影响。
对象仿真器PE训练的结果应使偏差函数JE最小。
对象仿真器PE执行训练,为了方便说明训练算法起见,考虑在采样序号为k的时刻的m维输入学习向量XEi(k-1-i),根据式(2.34)有
XE.i(k-1-i)=[y(k-1-i),...,y(k-p-i),u(k-1-i),...,u(k-q-1-i)]T (2.36)
在学习中,BP算法以下式表示
BP(ψ,X,y,yE,i)
其中:BP为四算法名称,为映射,x为输入向量,y为期望输出,yE,i为实际输出。
PF训练的算法过程如下:
Step1:READ y(k)
step2:{仿真器PE训练 }
i——t-1
REPEAT
yE,i——E(XE,i)
BP(ψE,XE,i,λiy(k-i),yE,i)
i——i-1
UNTIL(i<0)
Step 3:{产生控制信号u}
Xc——[r(k+1),y(k),...,y(k-p+1),u(k-1),...,u(k-q)]T or [r(k+1),r(k),...,r(k-p+1),u(k-1),...,u(k-q)]T
u(k)——ψc(Xc)
Step 4:以u(k)去控制对象,并持续Ts时间。
Step 5:{数据移动}
i——t-1
REPEAT
XE,i=XE,i-1
i——i-1
UNTIL(i=0);
Step 6:{产生最新数据向量}
XE,0——[y(k),y(k-1),...,y(k-p+1),u(k),...,u(k-q)]T
Step 7:k——k+1
Step 8:转向Step 1
对象仿真器PE训练例子:设k=10,则采样结果有y(10),并且取p=3,q=2,t=3.则在存贮器中存放有(p—1+t)=5个先前输出值y1即
y(9),y(8),……,y(5)
同时,有(q+t)=5个先前的控制值u,即
u(9),u(8),…,u(5)
则PE的输入学习向量为:
XE,0(9)=[y(9),y(8),y(7),u(9),u(8),u(7)]T
XE,1(8);[y(8),y(7),y(6),u(8),u(7),u(6)]T
XE,2(7)=[y(7),y(6),y(5),u(7),u(6),u(5)]T
用PEk·i表示取在采样时刻k时,第i次学习后的状态;用ψEk.i表示PEk·i所执行的映射.则有ψ10.0,ψ10.1,ψ10.2。
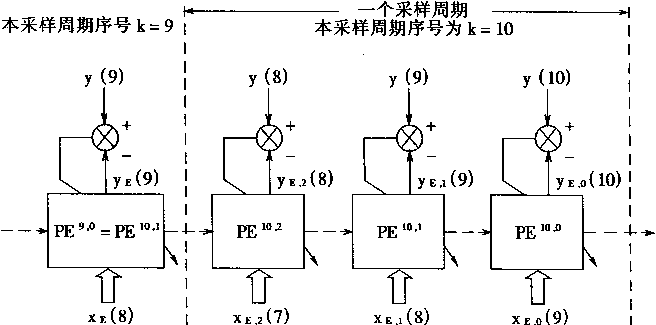
图2-12 对象仿真器PE的训练
根据式(2.35).对于第k时刻应有
yE,i(k-i)=ψEk,i[XE,i(k-1-i)] (2.37)
从而有
yE,0(10)=ψE10,0[XE,0(9)]
yE,1(9)=ψE10,1[XE,1(8)]
yE,2(8)=ψE10,2[XE,2(7)]
很明显,有
ψE9,0(.)=ψE10,1(.)
即有
ψEk,0(.)=ψEk+1,1(.)
在这个例子中,PE训练的情况如图2—12所示。
二、神经控制器NC训练学习
神经网络控制器NC的训练学习有两种不同的逼近方法, 一种是直接逆控制误差逼近(The Direct Inverse Control Error Approach),另一种是预测输出误差逼近(The Predicted Output Error Approach)。根据上述这两种不同的逼近方法其训练学习的过程不同。
1.直接逆控制误差逼近训练学习
假定在k+1采样时刻的现行输出为y(k+1);y先前的P-1+t个值,u先前的q+t个值存贮在存贮器中;有y(k)…,y(k-p+1-t);u(k)…,u(k-q-t)。
从图2—9所示的直接逆控制结构可知:可以用Xc*(k-i),u(k-i)数据对对神经网络控制器NC进行训练;其中
Xc*(k)=[y(k+1),...,y(k-p+1),u(k-1),...,u(k-q)]T (2.38)
当取i=0,1,…,t-1,时,显然有t对Xc*(k—i),u(k—i);它们用于k+1时刻对NC的训练。
k+1时刻的第i个m维输入学习向量为
X*c,i(k-i)=[y(k+1-i),......,y(k-p+1-i),u(k-1-i),......,u(k-q-i)]T (2.39)
则在神经控制器NC的输出有uc(k—i)
uc,i(k-i)=ψc[X*c,i(k-i)] (2.40)
考虑偏差函数Jc。
| (2.41) |
其中:1≥λ0≥λ1≥...≥λt-1
并有δk,i=-aJc/auc,i
δk,i=λi[u(k-i)-uc,i(k-i)] (2.42)
从式(2.41)看出,以Jc为训练时的偏差函数并不直接涉及系统的输出y的偏差。因此,会产生神经控制器NC训练结果为零偏差,但控制性能很差的效果。所以,为了克服这种问题,一般把直接逆控制误差最小化的训练方法和其它方法,例如与对象输出误差最小化的法相结合,从而使NC训练和控制性能效果都能取得良好的结果。为了便于说明神经控制器NC的训练.考虑在采样序号为k时的m维学习向量X*c,i(k-1-i)
X*c,i(k-1-i)=[y(k-i),y(k-1-i)...,y(y(k-p-i),u(k-2-i),...,u(k-q-1-i)]T (2.43)
在学习中,BP算法以下式表示
BP(ψ,X,u,uc,i)
其中:ψ为NC映射,x为输入学习向量,u为NC期望输出,uc,i为NC实际输出。
NC的训练算法过程如下:
Step 1:READ y(k)
Step 2:{取最新数据向量}
X*c,0——[y(k),...,y(k-p),u(k-2),...,u(k-q-1)]T
Step 3:{控制器训练}
i——t-1
REPEAT
uc,i——ψc(X*c,i)
BP(ψc,X*c,i,λiu(k-1-i),λiuc,i)
i——i-1
UNTIL(i<0)
Step 4:{产生控制信号u}
Xc=[r(k+1),y(k),...,y(k+1-p),u(k-1),...,u(k-q)]T or [r(k+1),r(k)...,r(k+1-p),u(k-1),...,u(k-q)]T
u(k)——ψc(Xc)
Step 5:用u(k)去控制对象,并持续T。
Step 6:{数据移动}
i——t-1
REPEAT
X*c,i——X*ci-1
i——i-1
UNTIL(I=0)
Step 7:K——k+1
Step 8:转向Step 1
用直接逆控制偏差逼近法对NC训练的例子:设现行采样时刻为k=9,故对象有输出y(9);取P=2,q=3,t=3,则在存贮器中存放有(p+t-1)=4个先前输出值y,即
y(8),y(7),y(6),y(5)
同时,有(q+1)=5个先前控制值u,即
u(7),u(6),u(5),u(4),u(3)
根据式(2.43),则NC的输入学习向量在k=9时有
X*c,0(8)=[y(9),y(8),y(7),u(7),u(6),u(5)]T
X*c,1(7)=[y(8),y(7),y(6),u(6),u(5),u(4)]T
X*c,2(6)=[y(7),y(6),y(5),u(5),u(4),u(3)]T
用NCk·1表示NC在采样时刻k时.第i次学习后的状态;用ψck.i表示NCk.i所实现的映射.则有ψc9.0,ψc9.1,ψc9.2
根据式(2.40),在第k采样周期中,有
uc,i(k-i)=ψck+1,i[X*c,i(k-i)] (2.44)
从而有映射结果:
uc,0(8)=ψc9,0[X*c,0(8)]
uc,1(7)=ψc9,1[X*c,1(7)]
uc,2(6)=ψc9,2[X*c,2(6)]
而训练NC时,有数据输入u(8),u(7),u(6)它们和uc,0(8),uc,1(7),uc,2(6)的偏差就组成了式(2.41)所示的偏差函数Jc。
在实际训练中需要把图2—10所示的直接适应控制或图2—11所示的间接适应控制方法和直接逆控制误差逼近方法相结合,才能实现取得对象输出误差最小的结果。
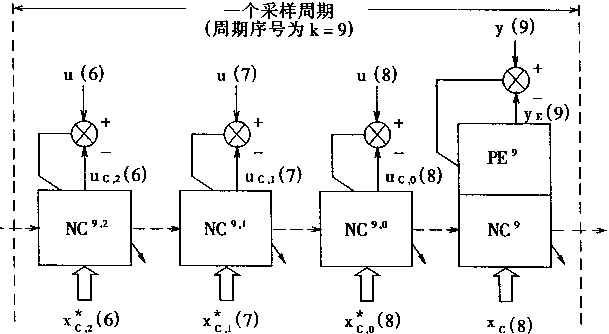
把间接适应控制的简单学习和直接逆控制误差逼近的多次学习相结合,从而在一个采样周期含有4个训练周期。这种情况如图2—13所示。
在图2—13中.左边3个学习训练过程是神经网络控制器NC单独学习的过程,其学习步骤在上面已经给出。而右边的1个学习训练过程是间接适应控制和直接逆控制误差逼近相结合的学习;由于这时采样时刻是k=9,故对象仿真器表示为PE9,神经控制器表示NC9在PE9和NC9相结合的学习中,输入的训练学习数据对为r(9),Xc(8),并有
Xc(8)=[r(9),y(8),y(7),u(7),u(6),u(5)]T
而r(9)是采样时刻k=9时的给定输入信号
(b)
图2-13 直接逆控制误差和间接适应控制逼近NC的过程
神经网络控制器NC在这时的状态用NC9表示.则其映射用ψc9,根据式(2.21)(2.22)从而有控制输出uc(8):
uc(8)=ψc9[Xc(8)]
对象仿真器PE这时的状态用PE9表示,则其映射用ψE9表示,这时有XE(8)
XE(8)=[y(8),y(7),y(6),uc(8),u(7),u(6)]T
从而有PE输出yE(9)
yE(9)=ψE9[XE(8)]
利用偏差eE.即eE=r(9)—yE(9),取偏差函数JE
JE=0.5[r(9)-yE(9)]2
则可以对NC进行训练学习。
2.预测输出误差逼近训练学习
直接逆控制误差逼近是以神经网络控制器NC输出的控制信号uc和期望控制信号u的误差进行逼近训练的。预测输出误差逼近的训练方法与之不同,它是以对象仿真器PE的输出yE和期望给定r的误差进行训练的,训练的对象是神经网络控制器NC。预测输出误差逼近训练学习的系统结构框图如图2—14所示。
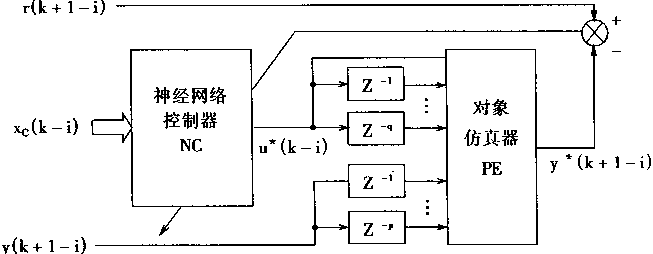
图2-14 预测输出误差逼近训练的结构
从图2—14所示结构可知:NC接收输入向量Xc,从而产生u*输出;而PE接收输入向量xE,xE由u*,y形成,从而产生输出y*。最后有
eE=r-y*
则可用于构成偏差函数J,用于训练。
假定在k+1采样周期内,给定值r有t个值存贮于存贮器中.即有
r(k+1-i) i=0,1,......,t-1
即是 r(k+1),r(k),......,r(k+2-t)
对象输出y有包括y(k+1)在内的p+t个值存于存贮器中,即有
y(k+1),y(k),y(k-1),......,y(k+2-p-t)
控制器输出u的先前q+t个值也存于存贮器中,即有
u(k-1),u(k-2),...,u(k-q-t)
从式(2.21)和式(2.23)可知在存贮器中等于存放了xc.i(k-i)
Xc,i(k-i)=[r(k+1-i),y(k-i),...,y(k-p+1-i),u(k-1-i),u(k-2-i),...,u(k-q-i)]T
或者
Xc,i(k-i)=[r(k+1-i),r(k-i),...,r(k-p+1-i),u(k-1-i),u(k-2-i),...,u(k-q-i)]T
在进入k+1采样周期时,神经网络控制器NC的状态为NCk+1,1,故其映射表示为ψck+1;对象仿真器PE不执行学习,其状态表示为PEk+1,映射表示为ψEk+1。
首先,在有输入向量xc.i(k-i)时,NC产生输出u*
u*(k-i)=ψck+1,i[Xc,i(k-i)] (2.45)
很明显,则在对象的输入形成向量X*E,i(k-i)
X*E,i(k-i)=[y(k-i),...,y(k-p+1-i),u*(k-i),...,u*(k-q-i)]T (2.46)
随后,则由对象仿真器PE输出预测值y*
y*(k+1-i)=ψEk+1[X*E,i(k-i)] (2.47)
最后,则可以得到预测偏差eE
eE=r(k+1-i)-y*(k+1-i) (2.48)
取偏差函数JE为
| (2.49) |
神经网络控制器NC训练过程可以理解如下:把NC和PE看成一个单一的多层神经网络MNN,在k+1采样周期中,每一个输入向量Xc.i(k—i),i=0,1,…,t-1;都会产生相应的预测偏差如式(2.48)所示。训练的目的就是使式(2.49)所示的偏差函数JE最小化。
神经网络控制器KC的预测输出误差逼近方法进行训练学习的过程中,考虑k采样时刻的输入向量Xc,i(k-1-i)
Xc,i(k-1-i)=[r(k-i),y(k-1-i),...,y(k-p-i),u(k-2-i),...,u(k-q-1-i)]T (2.50)
或者
Xc,i(k-1-i)=[r(k-i),r(k-1-i),...,r(k-p-i),u(k-2-i),...,u(k-q-1-i)]T (2.51)
在结构中,把NC和PE看成一个单一的网络,并且用(ψc+ψE)表示。则BP算法用下式表示
BP(ψc+ψE,X,r,y*)
其中:ψc+ψE为NC和PE组成的单一网络,x为输入学习向量,r为给定值即期望值,y*为预测输出。
NC的训练算法步骤如下:
Step 1:READ y(k)
Step 2:{NC通过预测误差逼近训练}
i——t-1
REPEAT
j——0
REPEAT
uj*——ψc(Xc,i+j)
j——j+1
UNTIL(j>q)
{产生PE的输入向量}
X*E,i——[y(k-1-i),...,y(k-p-i),u0*,u1*,...,uq*]T
{产生预测输出}
y*——E(X*E,i)
BP(ψc+ψE,Xc,i,λir(k-i),λiy*)
i——i-1
UNTIL(i=0)
Step 3:{用最新数据训练}
BP(ψc+ψE,Xc,0,λir(k),λiy(k))
Step 4:{数据移动}
i——t+q+1
REPEAT
Xc,i——Xc,i-1
i——i-1
UNTIL(i=0)
Step 5:{产生控制信号}
Xc,0=[r(k+1),y(k),...,y(k+1-p),u(k-1),...,u(k-q)]T or [r(k+1),r(k),...,r(k+1-p),u(k-1),...,u(k-q)]T
u(k)——ψc(Xc,0)
Step 6:用u(k)去控制对象,并持续T。
Step 7:k—k+1
Step 8:转回Step 1
下面给出一个用预测输出误差逼近方法训练NC的例子:假定现行采样周期为k=9,则有对象输出y(k),取P=2,q=3,t=3;则在存贮器中存有先前输出值y共(p+t-1)=4个,即y(8),y(7),y(6),y(5)
同时,有(q+t)=5个先前控制值u,即
u(7),u(6),u(5),u(4),u(3)
根据式(2.50),则有
xc.0(8)=[r(9),y(8),y(7),u(7),u(6),u(5)]T
xc.1(7)=[r(8),y(7),y(6),u(6),u(5),u(4)]T
xc.2(6)=[r(7),y(6),y(5),u(5),u(4),u(3)]T
参考图2—14所示的学习结构,则学习过程如图2—15中所示。
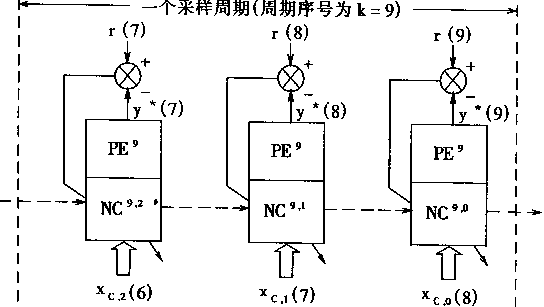
(a)
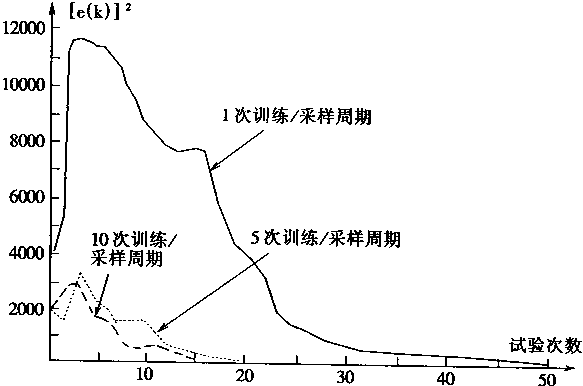
(b)
图2—15 预测输出误差逼近训练NC