4.2神经模糊控制系统
神经模糊控制系统是用神经网络作为控制器实现模糊推理控制的系统。
模糊控制系统有一个很明显的缺点:这就是它缺乏有效的学习机制。神经模糊控制系统的优异之处则在于可以用神经网络的学习机制补偿模糊控制系统原有的缺点;
神经模糊控制系统是以基于网络的适应模糊推理系统ANFIS(Adaptive Network-based Fuzzy Inference System)组成的。ANFIS也称适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System)。在前面有关章节中所介绍的神经模糊控制器也就是典型的ANFIS。
典型的反馈控制系统框图如图4—8所示,它由控制器和被控对象组成。被控对象一般由一组差分方程描述。这些方程说明了被控对象状态x(t)的特性。而对于控制器而言,通常是用g表示其静态函数,这也就是被控对象x(t)状态对控制作用u(t)的影射。
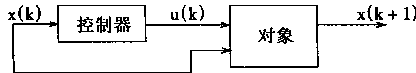
图4-8 反馈控制系统框图
对于框图,可以有以下方程
x(k+1)=f(x(k),u(k))
u(k)=g(x(k))
在控制工程中,其中心的问题是:为了达到预期的控制目的,就是要找出作为对象输出状态x的函数的控制作用u。
用神经网络构成模糊控制器,就是用神经网络实现模糊映射;并且对一个被控对象进行控制。
在这一节中,先介绍神经模糊控制系统的有关结构,再介绍神经模糊控制系统的具体应用情况。
4.2.1 神经模糊控制系统结构
神经模糊控制系统的结构是和所采用的控制方式有关的。神经模糊控制有多种不同的控制方式,这些方式包括模仿经验控制,逆控制,专门学习控制,反馈线性化及滑模控制,其它方式控制。在这一部分,分别简要介绍这些控制方式及控制系统的结构。
一、模仿经验控制
模仿经验控制在本质上是把人们的经验加以总结,然后用神经模糊控制器模仿人的有关经验,从而实现对被控对象的控制。模仿专家的经验进行控制是模糊控制器的本来的目的。对一些复杂的系统,例如化学反应过程,地下铁道,交通系统等,人类的专家可以很好的实现控制,神经模糊控制器可以模仿这些专家,实现对复杂系统的有效控制。
一船而言,专家给出的经验是以模糊条件语句的方式给出的,而条件语句中的模糊量隶属函数也较粗糙;所以在应用时还需要进行较多的试验和误差处理,以重新定义隶属函数。
采用神经模糊控制器来进行模仿经验控制,则可以采用神经网络的学习机制,并利用其对数字信息,如输入输出数据的学习处理,从而可以对隶属函数进行重新定义。最后,取得较合理的结果。
这种方法不但可以用于控制系统;如果,目标系统可以用人类经验进行模仿;那么.所得到的模糊推理系统是模糊专家系统。故而,这种方法也可以用于系统诊断和分析。
二、逆控制
逆控制是神经模糊控制的一种控制方式,这种控制方式来自于神经网络控制方法。
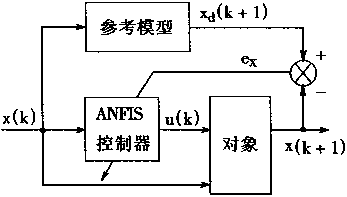
神经模糊逆控制的作用如图4—9所示。为了简便起见,假设被控设备只有一个输出状态x(k)和一个输人u(k)。控制分成两个阶段:即学习阶段和应用阶段。
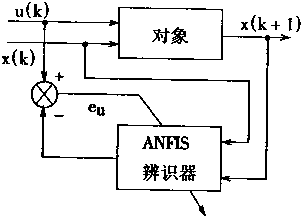
(a) |
(b) |
图4-9 神经模糊逆控制
在学习阶段,采用随机输入集,可以得到被控对象所产生的相应输出。学习阶段如图4-9(a)所示。在图中,ANFIS用于学习被控对象的逆模型。在学习时,采用随机输入信号u(k)以及输出信号x(k),x(k+1)这些信息。
在应用阶段,系统的结构如图4—9(b)所示。被控对象的逆模型用作控制器直接对被控对象进行控制。如果对象的逆模型是精确的,也即是x(k),x(k+1)到u(k)的映射是精确的,确的,则用u(k)去对对象进行控制必定能产生结果x(k+1)。这个结果会逼近给定xd(k)。这个系统在控制的角度讲是一个纯单周期延时系统。
这种控制方法看起来只需一个唯一的学习任务,也就是寻找对象的逆模型。这就要求有一个先决的条件,即对象的逆模型存在。但是,并非所有的对象存在逆模型.进一步讲,网络络误差[cu(k)]2的最小化并不能确保整个系统误差‖xd(k)-x(k)‖2的最小化。
要克服这个问题,可采用ANFIS构成适应逆控制系统。
三、专门学习控制
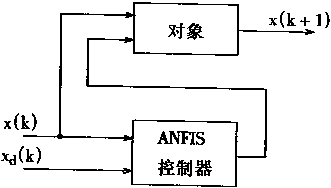
逆控制所存在的主要问题是以神经网络的误差最小化取代整个系统的误差最小化。在神经模糊控制中,直接使系统误差最小化的一种方法是所谓“专门学习”方法。这种方法如图4-10中所示:
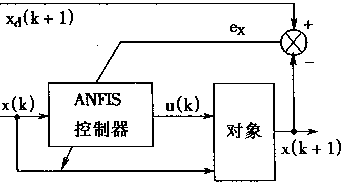
(a) |
(b) |
图4-10 神经模糊逆控制
为了使反向传播误差信号通过图4—10中的对象框图,故而需要求取可以代表对象性能的模型。事实上,为了采用BP学习算法,需要知道对象的雅可比矩阵(Jacobian matrix),在该矩阵中,其i行j列的元素等于对象的第i次输出对其第i次输入的导数。
如果对象的雅可比矩阵不容易求取,则可以在两个连续的时刻对对象在线进行输入和输出变化处理,以估计雅可比矩阵。
专门学习控制的结构如图4—10(a)中所示。给定信号为xd(k+1),在ANFIS控制器中输入系统的输出x(k),然后把ANFIS输出u(k)以及系统输出x(k)作为对象的输人。把对象输出x(k+1)和给定信号xd(k+1)进行比较,产生的误差ex用于对ANFIS控制器校正。校正过程采用BP算法。很明显,这是以整个系统的误差最小化为目标进行学习的。
通常人们不习惯在每个时刻k去表明所需的对象输出x(k),在参考模型适应控制中,所需的整个系统的性能可以用一个通常是线性的模型来表示,这个模型可以成功地满足控制目的。这种方法如图4—10(b)中所示。在图中,所需的输出xd(k+1)通过所需模型产生。
四、反馈线性化及滑模糊控制
在连续时间域中,动态系统的运动方程可以用典型的形式表达如下
x(n)(t)=f(x(t),x(t),x(2)(t),......,x(n-1)(t))+bu(t) (4.39)
其中:f是未知连续函数,
b是控制增益。
系统控制的目的是使状态向量
X=[x,x,x(2),......,x(n-1)]T (4.40)
即随所需的轨迹
Xd=[xd,xd,xd(2),......,xd(n-1)]T (4.41)
如果定义误差向量为
e=X-Xd (4.42)
则控制目的是设计一个控制u(t),使得在t——∞时,e——0。
如果f是已知的,则式(4—39)可以简化为线性系统,故它是一个典型线性化系统。
在f已知时,采用下面控制u(t):
u(t)=-f(X(t))+Xd(n)+kTe (4.43)
将把原有的非线性系统转换成线性系统:
e(n)(t)+k1e(n-1)+……+k(n-1)e+kn=0 (4.44)
这里,K=[kn,k(n-1),……,k1]T是恰当选择的向量,它应保证满足式(4.44)闭环线性系统的特性。
但在式(4.39)中,f是未知函数,从直觉上应选择控制u(t)为:
u(t)=-F(X,p)+xd(n)+kTe+V (4.45)
其中:F是足以逼近f的参数化函数,
V是附加输入。
当采用控制u(t)时,则得到的闭环系统按如下求出:
1.在式(4.43)中,kTe满足式(4.44),即有:
u(t)=-f(X(t))+xd(n) (4.46)
2.从式(4.45),(4.46)则有
-f(x(t))+xd(n)=-F(X,p)+xd(n)+kTe+V
从而有
kTe=F(X,p)-f(X(t))-V
即有:
e(n)+k1e(n-1)+......+k(n-1)e+ku=(F-f)-V (4.47)
式(4.47)表述了用式(4.45)所示的控制时得到的闭环系统。
很显明,存在两个问题:
1.需要逐渐修改参数向量P,使到对于所有的X,有F(X,p)≈f(x)
2.在F逼近f的整个过程中,需要加上附加控制V以保证总体稳定性。
解决策一个问题不难,采用模糊神经网络就可以通过参数学习逼近f。
解决第二个问题则可以采用滑模控制。
这种控制方式只能用于反馈可线性化的系统。
五、其他控制方式
其它控制方式还有增益排表控制(Gain Scheduling Control),随机方法,增强学习(Reinforcement learning)法等。增益排表控制一般用于一阶Sugeno模糊模型,而随机方法一般用于复杂控制系统。对于对象模型不清楚的或不是很有效的,则可以用增强学习方法。
4.2.2典型的神经模糊控制系统
神经模糊控制系统可以用多种神经网络来实现。这些神经网络可以是正向前馈网络,也可以是反馈网络。既可以用模糊神经网络,也可以用径向基函数,也可以用单向线性响应函数作为激发函数的神经元。在这一节中,给出两十分典型的例子,一个是采用模糊推理网络的例子,一个是采用单向线性响应激发函数的例子。它们构成了结构不同的神经模糊控制系统。而它们各自有着明显不同的特点,但在学习上都是取得较好的效果。
一、模糊推理网络构成的控制系统
这是一个采用简化模糊推理网络SFIN(Simplified Fuzzy Inference Network)组成的神经模糊控制系统,由于采用了神经网络,故而在系统中的控制器是自校正模糊逻辑控制器STFLC(Self-Tuning Fuzzy Logic Controller)。下面对这个系统进行简要介绍。
1.简化模糊推理网络
模糊逻辑控制器是执行Takagi-Sugeno推理的控制器.考虑控制器为多输入单输出结构。控制规则有如下形式:
if X is Ai then yi=fi(X)
其中:X=[x1,x2,......,xm]T
Ai=[A1i,A2i,......,Ami]
fi(X)=[P0i+P1ix1+......+Pmixm]
i=1,2,......,n。
在控制规则中,X是输入;Ai是模糊量;Aki是第k一个输入分量xk的第i个模彻量。fi(X)是对应于输人x的输出,Pki是第6规则中后件二项式中的输入量系数。
对于第i条规则,其匹配度用Di表示,并且有
Di=A1i(x1)*A2i(x2)*......*Ami(xm) (4.48)
其中:x1,x2,……,xm为输入精确量
A1i(x1)为x1对A1i的隶属度,其余A1i(x2),……,Ami(xm)同理。
所有的控制规则产生的总输出为y:
| (4.49) | |
| 模糊量Aki(xk)用钟形函数或高斯函数表示,故而有: | |
| (4.50) |
或者
Aki(xk)=exp(-{[(xk-aki)/bki]2}cki) (4.51)
其中:aki,bki,cki是函数的参数;改变这些参数则函效会产生相应的变化。故而模糊量的形状也产生变化。
当系统是一个双输入单输出系统时,则模糊推理网络的结构如图4—11所示。
在这个网络中有两个输入,每个输入被划分成3个模糊量。对于输入x1,有L1(大),M1(中),s1(小)这3个隶属函数;对于输入x2,有I2(大),M2(中),S2(小)这3个隶属函数。故而有9条控制规则:
if x1 is L1 and x2 is L2 then y1=f1(x1,x2)
if x1 is L1 and x2 is M2 then y2=f2(x1,x2)
if x1 is L1 and x2 is S2 then y3=f3(x1,x2)
if x1 is M1 and x2 is L2 then y4=f4(x1,x2)
if x1 is M1 and x2 is M2 then y5=f5(x1,x2)
if x1 is M1 and x2 is S2 then y6=f6(x1,x2)
if x1 is S1 and x2 is L2 then y7=f7(x1,x2)
if x1 is S1 and x2 is M2 then y8=f8(x1,x2)
if x1 is S1 and x2 is S2 then y9=f9(x1,x2)
对应于图4—11中的模糊划分,则输入空间被划分成9个模糊子空间,如图4—12中所示。
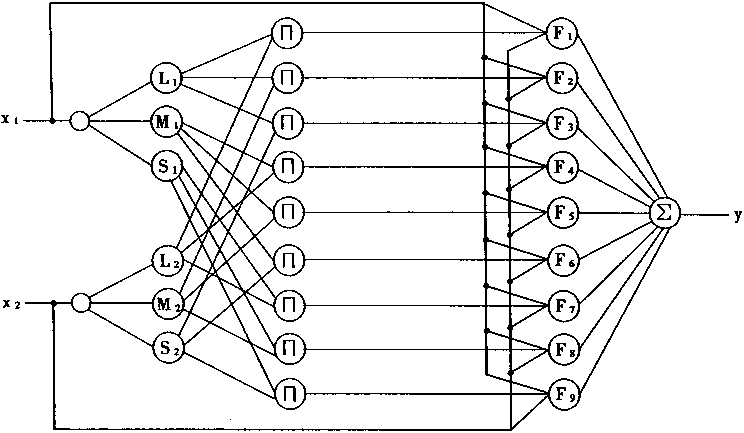
图4-11 简化的模糊推理网络SFIN
图4—11所示的模糊推理网络表示的控制规则中,由于只有两个输入,故而有
yi=fi(X)=fi(x1,x2), i=1,2,......,9
即是:yi=p0i+p1ix1+p2ix2 (4.52)
如果对图4—11所示的网络进行优化,则相应对于控制规则的前件和后件进行优化。
当对控制规则进行前件优化时,也即对网络的第二层神经元进行优化,这时也即是对径向基函数的参数aki,bki,cki进行优化;其中k是输入量下标号,即k=1,2,i是控制规则条数号,即i=1,2,…,9。从控制规则集中可知,有模物量:
A11=A12=A13=L1 A21=A22=A23=L2
A14=A15=A16=M1 A24=A25=A26=M2
A17=A18=A19=S1 A27=A28=A29=S2
当对控制规则的后件进行优化时,也即是对fi(x1,x2)中的系数p0i,p1i,p2i进行优化。
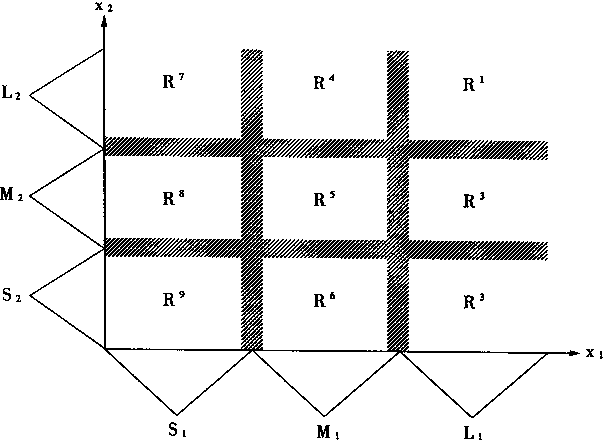
图4-12 模糊子空间
2.神经模糊控制器的优化
当在简化的模糊推理网络SFIN中的X1端输入偏差信号e(k)=yd(k)-y(k);其中yd(k)为给定信号,y(k)为对象实际输出信号。在x2端输入偏差变化率Δe(k)=e(k)-e(k-1)。而在SFIN输出端输出的是增量控制信号Δu(k)=u(k)-u(k-1)。则SFIN可以看作一个参数化的模糊控制器。
对SFIN考虑二个优化过程。一个是SFIN初始化的监视学习优化;另一个SFIN的在线自适应学习优化。
(1)SFIN的初始化监视学习
给出用于SFIN初始化的教师信号数据。
T{[e(i),Δe(i)]——Δu(i)|i=1:N} (4.53)
其中:e(i),Δe(i)是输入
Δu(i)是输出。
初始化教师数据来自系统控制人员的控制数据,优化时采用的目标函数为I0:
| (4.54) | |
| 其中:SFIN[e(i),Ae(i)]表示数据对e(i),Ae(I)输入SFIN之后得到的输出。 用W表示SFIN中的普通参数,它可以用下式进行校正: |
|
| (4.55) |
其中:η(k)是学习速率,1>η(k)>0。
(i)前件参数估计
偏差e所取的模糊量个数表示为Ne。i偏差变化率Δe所取的模糊量个数表示为NΔe。
根据先验知识,偏差e和偏差变化率Δe的边界分别是:
Se≤e≤Be
SΔe≤Δe≤BΔe
则前件的初始参数可以选择如下
![]()
![]()
![]()
(ii)后件参数估计
从上可知,在SFIN中有控制规则为Nr条:
Nr=Ne*NΔe (4.56)
由于控制规则的后件为yi=fi(x)=p0i+p1ix1+p2ix2,也即有参数p0i,p1i,p2i。所以,总的后件参数为Ng;
Ng=3Nr (4.57)
要求取Ng个参数,则要求有Ng个输入输出教师数据对:
{[e(q),Δe(q)]——Δu(q)},q=1:Ng (4.58)
并通过这Ng个数据对才能形成Ng个方程的方程组.以求取后件的Ng个参数。
当在SFIN输入Ng对[e(q),e(q)],q=1:Ng数据时,则从式(4.49)有:
| (4.59) | |
| 在上面式(4.59)中,需要求fi中的参数p0i,p1i,p2i,则可写成 | |
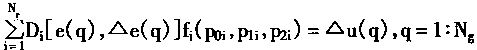 |
(4.60) |
用P表示后件fi的参数向量.M为Di的Ng*Ng短阵.U=[Δu(1),Δu(2),……,Δu(Ng)]T,则式(4.60)可以写成如下矩阵形式:
MP=U (4.61)
显然,解矩阵方程式(4.61),则有
P=M-1U
从而可得后件参数向量P,也即得出后件参数,p0i,p1i,p2i,i=1:9。
(2)SFIN的在线自适应学习优化
模糊推理网络SFIN是作为模糊控制器的,由它组成的模糊控制系统的框图如图4-13所示。

图4-13 模糊控制系统
在给出了SFIN的初始化参数之后,则可以对SFIN进行在线自适应学习优化。在优化时采用如下性能指标:
| (4.62) | |
| 其中:h是偏差平方累加个数, l是加权控制增量平方累加个数, θ(i)是加权因子。 在上式中yd(k-i)-y(k-i)=e(k-i),即偏差。 在线自适应时系统SFIN中参数W的校正采用下式 |
|
| (4.63) |
在式(4.63)中,对J(k)的偏微分求取如下
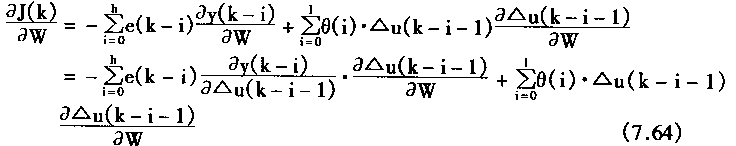
很明显aJ(k)/aw和aΔu(k-i-1)/aw成比例.即有
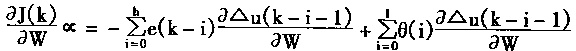 |
(4.65) |
| 在上面式子中,Δu(k-i)是可从神经网络的输出求得的 | |
| Δu(k-i)=SFIN[e(k-i),Δe(k-i);W(k)] | (4.66) |
3.控制系统的运行结果
对于给定的对象,采用SFIN可实现神经模糊控制并取满意的结果。
(1)被控对象PL
被控对象PL表示如下:
PL(V1,V2,V3,V4,V5,yd)
其中:yd是设定的期望点。
被控对象的输入输出关系由下式表示
yk+1=f(yk,yk-1,yk-2)+g(k,yk-3,yk-4,Uk-2)+(1.1+V1)uk-1+(1+V2)uk+Zk (4.67)
其中:
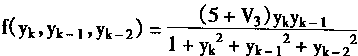 |
(4.68) |
g(k,yk-3,yk-4,Uk-2)=V4Sin[0.08(yk-3+yk-4)]Uk-2+V5cos(0.05kπ) (4.69)
g(·)是干扰信号,
Vi(i=1,2,…,5)是实参数。
Zk是白噪声,其最大幅值为0.1。
(2)训练数据集
给出的训练数据集如表4—1所示,它一共有30组训练数据。这些数据用于对SFIN进行初始化监视学习,从而确定SFIN的初始参数。
表4-1 数据训练集
| k | E(k) | ΔE(k) | ΔU(k) | k | E(k) | ΔE(k) | ΔU(k) |
| 1 | 3.0000 | 0.0000 | 0.1893 | 16 | -0.1472 | -0.5316 | 0.0462 |
| 2 | 2.8228 | -0.1772 | 0.1732 | 17 | -0.2259 | -0.0787 | 0.0024 |
| 3 | 2.3440 | -0.4788 | 0.1421 | 18 | -0.1874 | 0.0385 | -0.0040 |
| 4 | 1.6426 | -0.7014 | 0.1063 | 19 | 0.0424 | 0.2298 | 0.0079 |
| 5 | 0.5628 | -1.0798 | 0.0578 | 20 | 0.1303 | 0.0879 | 0.0116 |
| 6 | -0.1911 | -0.7539 | 0.0255 | 21 | 5.0000 | 0.0000 | 0.5576 |
| 7 | -0.5456 | -0.3545 | -0.0058 | 22 | 4.4161 | -0.5839 | 0.4120 |
| 8 | -0.2664 | 0.2792 | -0.0061 | 23 | 3.3792 | -1.0370 | 0.2718 |
| 9 | -0.2132 | 0.0532 | -0.0031 | 24 | 1.5370 | -1.8442 | 0.1901 |
| 10 | -0.0111 | 0.2021 | 0.0030 | 25 | 0.3928 | -1.1442 | 0.0687 |
| 11 | 4.0000 | 0.0000 | 0.3415 | 26 | -0.3001 | -0.6930 | -0.0643 |
| 12 | 3.6478 | -0.3522 | 0.2901 | 27 | -0.1572 | 0.1429 | 0.0465 |
| 13 | 2.8956 | -0.7522 | 0.2093 | 28 | 0.1582 | 0.3154 | 0.0102 |
| 14 | 1.5613 | -1.3242 | 0.1322 | 29 | 0.2118 | 0.0535 | 0.0367 |
| 15 | 0.3844 | -1.1769 | 0.0893 | 30 | 0.2653 | 0.0535 | 0.0207 |
(3)自适应在线学习及结果
考虑对有关的参数学习时所选取的值如下:
前件有关参数有偏差e的模糊量参数ae,be,ce;偏差变化率Δe的模糊量参数aΔe,bΔe,cΔe,在学习这些参数时的学习速率η分别选值为
ae,aΔe,ce,cΔe的学习速率η=10-6
be,bΔe学习速率η=10-8
后件有关参数是其二项式参数P,它的学习速率η=0.00125。
在学习时所用的式(4.65)中的参数取:
h=1 l=0 θ=15
同时,学习公式(4.63)的迭代步数取3。
系统运行的情况如图4—14所示。
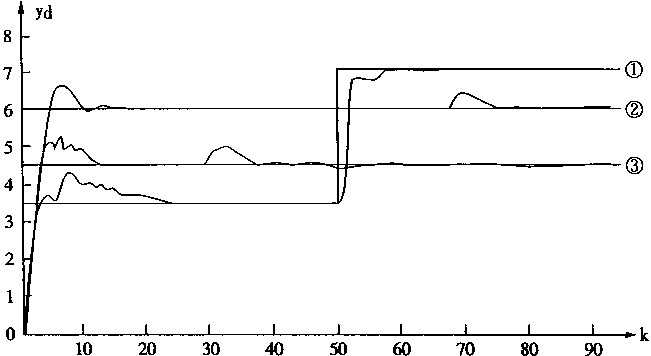
图4-14 较大干扰时SFIN运行情况
在图4—14中分别给出了3条响应曲线,这3条响应曲线分别用①②③标记。
对于响应曲线①,它是把设定点在k=50时进行改变的响应情况。这时被控对象参数变化如下:
PL(0,0,0,0,0,3.5)——PL(0,0,0,0,0,7.0)
对于响应曲线②,它是在k=70时参数改变所产生的响应情况。被控对象参数改变如下:
PL(0,0,0,0,0,6.0)——PL(-0.25,0.45,0.5,0,0,6.0)
对于响应曲线②,它是在k=30时产生干扰的响应情况。被控对象参数改变如下
PL(0,0,0,0,0,4.5)——PL(0,0,0,0.35,0.25,4.5)
单向线性响应URL(Unidirectional Linear Response)神经元可以构成模糊神经网络,从而可以构成神经模糊控制器。在这一节中介绍用URL模糊网络控制的控制系统。
1.URL模糊网络
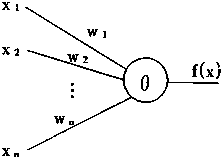
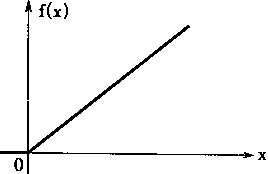
ULR神经元是在输入信号取值为正时有线性特性,而输人为负时则输出为零的神经元。URL神经元的结构和特性可用图4—15说明。在图中,(a)是神经元结构,可见它和一般神经元是一样的;(b)是神经元特性.可见它取正值时为线性,而输入取负值时则输出为零。
(a) |
(b) |
图4-15 URL神经元及特性
在图4—15中,x1,x2,……,xn是输入的模糊变量,Ux1,Ux2,……,Uxm分别是对应的隶属函数,Wi是xi,i=1,2,……,n和神经元的连接权系数,θ是阀值,f(x)是神经元的输出,则有:
| (4.70) | |
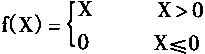 |
(4.71) |
采用URL神经元组成单层或多层神经网络,并可以实现各种基本或组合的模糊逻辑函数。
例1 用URL网络实现模糊蕴含关系:
![]()
考虑URL网络的结构如图4—16所示。它一共有3个URL神经元,并分为2层。输人有2个模糊量Ux+Uy。
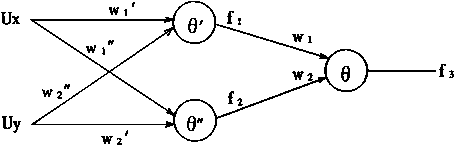
图4-16 URL网络
很明显,作为输出Ux——y=f3,即有
| (4.72) |
令
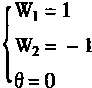
故有:![]()
从图4—16中,可以看出f1、f2的求取如下:
f1=f(W1'Ux+W2"Uy-')
f2=f(W1"Ux+W2'Uy-")
令
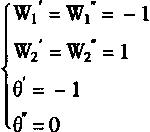
f1=f(-Ux+Uy+1)
f2=f(-Ux+Uy)
显然
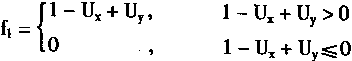
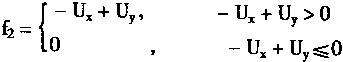
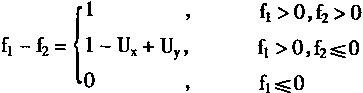
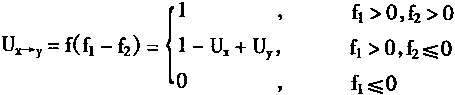 (4.73)
(4.73)
从式(4.73)中可知,当f1>0,f2≤0时有
![]()
这时,由于有f2≤0,即有
-Ux+Uy≤0
也即是 1-Ux+Uy≤1
故而式(4.73)表明ULR网络实现的功能为
![]()
例2 用ULR网络实现有界和功能Ux⊕y=1Λ(1-Ux+Uy)。
采用图4—16的同一ULR网络,并且令:
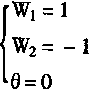
则有
Ux⊕y=f(W1f1-W2f2-θ)
=f(f1-f2)
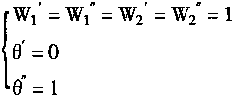
则有
f1=f(Ux+Uy)
f2=f(Ux+Uy-1)
显然
f1=Ux+Uy
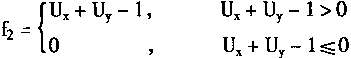
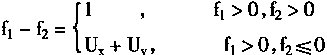
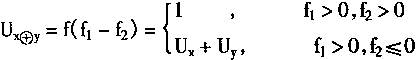 (4.74)
(4.74)
当f2≤0时,有Ux+Uy-1≤0,即
Ux+Uy≤1
故而有
Ux⊕y=1Λ(Ux+Uy)
可以由URL网络实现。
2.ULR模糊控制器
ULR模糊控制器是用ULR网络实现模糊推理规则的,图4—17给出了一个含有4条控制规则的ULR网络,在这个控制器中采用局部最大平均法LMOM(Localized Mean of Maximum Method)进行精确化。
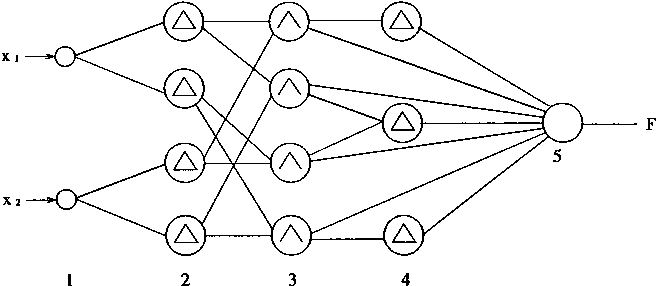
图4-17 ULR模糊控制器
在图4—17中,一共有5层结构,在每一层中,神经元的作用是相同的,在下面分别介绍各层的作用:
(1)第1层
这是输入节点,它不执行任何操作。
(2)第2层
这是隶属函数层,它是控制规则中前件的模糊量的隶属函数。控制规则有如下形式:
if x1 is A1i and x2 is A2i then y is Bi
在这一层中,神经元表述了UA1i、UA2i等隶属函数。在这一层中,得到的对应于输入的隶属度、UA1i(x1)、UA2i(x2)。
在ULR网络中,采用三角隶属函数。所以在这一层中,每一个节点也是用一个URL网络构成的。ULR网络实现三角隶属函数的结构如图4—18所示。
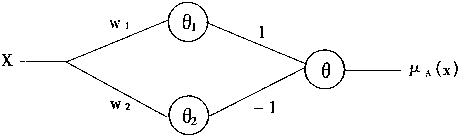
图4-18 ULR网络实现的三角隶属函数
对于三角隶属函数,所表达的方法如下;
对于三角隶属函数可以用其高的横坐标交点c,c点到右边顶角的距离R,c点到左边顶角的距离L这三外参数表示。故而,有三角隶属函数的图形如图4—19所示。
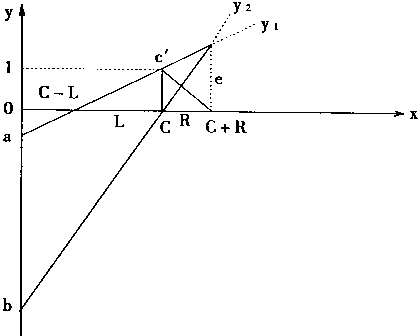
图4-19 三角隶属函数的形状