从图4—19可以看出
| (4.75) |
![]()
由于
![]()
![]()
故而
| (4.76) |
对于y1,根据ULR特性,在输入x<C-L时,输出为0。
对于y2,根据ULR特性,在输入x<C时,输出为0。
如果用y1—y2为输入,则有:
①x<C-L时,输出为0
②x<C时.输出为y1
③x<C+R时,输出为y1-y2
④x≥C+R时,有y1-y2<0,故输出为0。
很明显:可以得到(C-L),C',,(C+R)三点组成的三角形,对于上图4-18,如果令
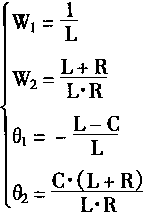
则有
![]()
![]()
利用y1,y2可以实现三角隶属函数功能,只要修改参数R、L、C,则可以实现不同的三角隶属函数。
(3)第3层
这是前件运算层,执行最小运算Λ.这一层采用二层ULR神经网络形成。如图4-20所示。
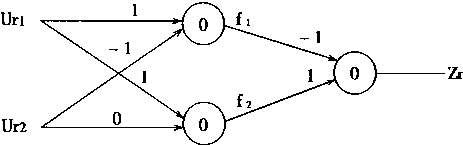
图4-20 前件最小化运算
从图4-20中,可知其功能为:
f1=f(Ur1-Ur2-0)=f(Ur1-Ur2)
f2=f(Ur1-0)=f(Ur1)
Zr=f(-f1+f2-0)=f(-f1+f2)
下面分别分析三种不同的输人情况:
①当有Ur1<Ur2时
f1=f(Ur1-Ur2)=0
f2=f(Ur1)=Ur1
从而有
Zr=f(-f1+f2)
=f(0+Ur1)
=Ur1
②当有Ur1>Ur2时
f1=f(Ur1-Ur2)=Ur1-Ur2
f2=f(Ur1)Ur1
则
Zr=f(-f1+f2)
=f(-Ur1+Ur2+Ur1)
=Ur2
当有Ur1=Ur2时
f1=f(Ur1-Ur2)=0
f2=f(Ur1)=Ur1
则
Zr=f(-f1+f2)=f(Ur1)=Ur1
从上可知:图4—20的URL网络实现了最小化运算。
(4)第4层
这是后件运算层,它执行两种操作。一种是把前件最小化运算结果再对后件模糊量求最小运算;另一种操作是执行反模糊化。这两种操作那是由局部最大平均法LMOM(Local Mean-of-Maximum)反模糊化方法实现的。
LMOM方法可以用图4—21进行说明。
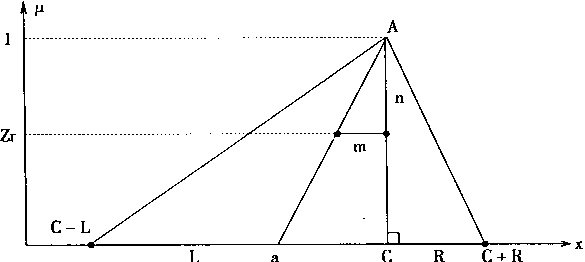
图4-21 LMOM法反模糊化
在图4—21中,a是三角形(C-L),A,(C+R)的底边的中点,故a的坐标为
![]()
当隶属度为1时,反模糊化的结果为C。
当隶属度为0时,反模糊化的结果为![]() 。
。
当隶属度为Zr时,则有
![]()
即
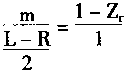
![]()
反模糊化的结果为:(C-m)
![]() (4.77)
(4.77)
设后件三角隶属函数为r,前件最小化结果为Zr,则反模糊化结果用Ur-1(Zr)表示,有
![]() (4.78)
(4.78)
反模物化可采用下面图4—22的结构。
![]()
图4-22 反模糊化接点
在图中取
![]()
显然有
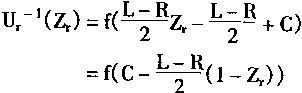
由于
![]()
故而
![]() (4.79)
(4.79)
(5)第5层
最后输出判决层。输出采用规则前件的最小隶属度为加权系数,对本规则的后件反模糊化结果进行加权,取加权平均值为最后判决结果F。
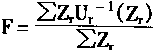 (4.80)
(4.80)
3.ULR模糊控制器学
ULR模糊控制器中,需要学习要是含有隶属函数的第2,4两层。
在学习时,目标函数用Q表示,而隶属函数的参数用P表示,学习的目的就是使目标函数Q达到最小。一般目标函数Q用输出的期望与实际误差来描述。
用梯度法对URL网络的第2,4层进行学习.就是按-aQ/aP方向修改参数P,即
| (4.81) | |
| 由于Q有时较为复杂,在修改时要首先考虑aQ/aP,也可写作 | |
| (4.82) | |
| 在上式中.aQ/aF为了方便起见可以用下式求取 | |
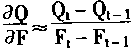 |
(4.83) |
显然,这是可以直接求得的。
下面分别对第2,4层中隶属函数的学习进行说明
对于第4层的隶属函数学习,其算法如下:
由于第5层输出为F,并且
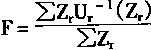
而第4层输出为Ur-1(Zr),并且
![]()
则有
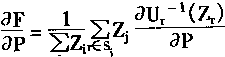 (4.84)
(4.84)
![]() (4.85)
(4.85)
![]() (4.86)
(4.86)
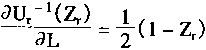 (4.87)
(4.87)
其中:Sj是第j条规则的语言变量,r是语言变量值。
显然.采用式(4.84)—(4.87),可求aF/aP。
对于第2层而言,如果要求aF/aP,则应考虑:
![]() (4.88)
(4.88)
其中:Uri是第2层的输出
由于
![]() (4.89)
(4.89)
其中:Ak是第k条规则的前件语言变量
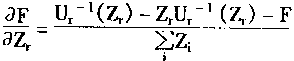
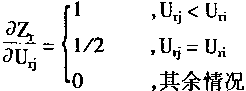
其中:Ur-1(Zr)是Ur-1(Zr)的导数。
同时,根据式(4.75)、(4.76)则aUri/aP很容易求取。
这样则对于第2层;aF/aP可以求出。
在式(4.82)中,由于aQ/aF,aF/aP都在第2,4层可以求出,故而能对这两层的隶属函数进行学习。一般aQ/aF不取实际值.只取其符号,即有:
![]()
最后有:
![]()
4.ULR模糊控制器对倒立摆的控制
对倒立摆的控制采用下列9条由条件语句组成的控制规则实现.如表4—2所示。
|
控 制 |
角度变化率Δθ | |||
| PO2 | ZE2 | NE2 | ||
|
角 度θ |
PO1 | PL | PM | ZE |
| ZE1 | PS | ZE | NS | |
| NE1 | ZE | NM | NL | |
角度θ是倒立摆和平衡位置的夹角,它的范围取-12°—+12°。角度变化率Δθ的范围取每秒-12°,即-12°/S,到每秒+12°,即+12°/S。
倒立摆安装在一个小车上,为了使倒立摆能处于平衡状态,故而要对小车进行控制。
角度θ,角度变化率Δθ以及控制的模糊量都是取三角隶属函数,它们的参数分别如表4—3中所示。
表4-1 隶属函数
|
模糊量 |
C | L | R |
| PO1
ZE1 NE1 |
0.3
0.0 -0.3 |
0.3
0.3 5000 |
5000
0.3 0.3 |
| PO2
ZE2 NE2 |
1.0
0.0 -1.0 |
1.0
1.0 5000 |
5000
1.0 1.0 |
| PL
PM PS ZE NS NM NL |
20.0
10.0 5.0 0.0 -5.0 -10.0 -20.0 |
5.0
5.0 4.0 1.0 5.0 6.0 0.0 |
0.0
6.0 5.0 1.0 4.0 5.0 5.0 |
模糊控制器的输入有角度和角度变化率,它们都归一化到[-1,1]区间。实际控制的结果如图4—23中所示。从图中可知,在执行了大约500步左右工作,则可以达到平衡状态,图中给出的是初始角度不同时的工作过程状态。
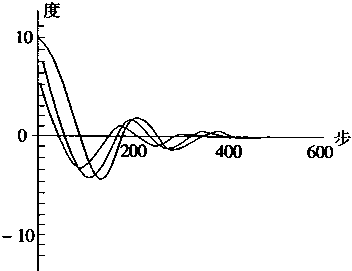
(a) |
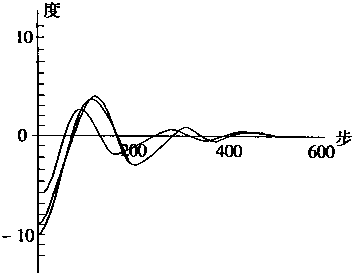
(b) |
|
图4-23 倒立摆平衡仿真结果 | |