2．3 神经网络控制系统

神经网络控制系统在本质上讲是由神经网络构成控制器的控制系统。这种控制系统最吸引人之处是在于控制器具有学习功能，从而可以对不明确的对象进行学习式控制．使对象的输出与给定值的偏差趋于无穷小。

在这一节中，介绍几个实际具体的神经网络控制系统，井给出这些系统的控制结果。

2．3．1 离散系统的神经适应控制

对于一个线性离散系统，进行神经适应控制时，其系统的结构框图如图2—16所示。在图中可以看出：它包括神经网络控制器NC，对象仿真器PE和学习机构，以及被控对象。PE的输入有控制量u和对象输出量y两种，NC的输入则有给定值r、本身的输出U和对象输出量y。系统中的NC和PE都是在工作中执行联机学习的，这是一个实时学习的控制系统。

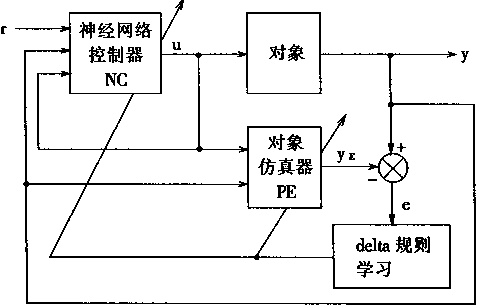
图2-16 离散系统神经控制结构

一、被控对象

被控对象可以用下面线性方程表示

A(q^-1)y(k)=B(q^-1)u(k) (2.52)

其中：

A(q^-1)=1+a₁q^-1+...+a_nq^-n；

B(q^-1)=b₁q^-1+...+b_mq^-m；

q^-1是延时算子，q^-1y(k)=y(k-1)；

y(k)是输出；

u(k)是输入。

对于被控对象的表达式，它满足下列3个条件：

1．m，n是有上界的，并且已知。

2．B(q-1)是一个稳定的多项式。

3．系数b₁≠0。

m．n有界，则可以明确用其上界值构造NC和PE的输入，从而得出具体的NC和PE，便于实际有效训练。B(q-1)稳定，则可保证控制器的闭环控制稳定。b₁≠0，是控制器所需的。

二、对象仿真器和神经控制器

对象仿真器PE和神经控制器NC都用线性神经网络构成。而且在结构上，都是一个输入层和一个输出层，而没有中层隐层的2层神经网络所构成。

1．对象仿真器PE

对象仿真器PE的结构如图2—17所示。在图中可看出：PE的输入向量为x(k-1)，输出为y(k)．权系数向量为w(k-1)。

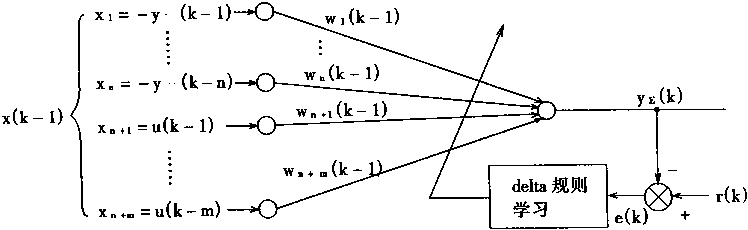
图2-17 对象仿真器PE的结构

考虑在k时刻，则这时有输入向量x(k)

x(k)＝[x₁(k)，x₂(k)，…，x_n(k)，x_n+1(k)，…，x_n+m(k)]^T
＝[-y(k)，…，-y(k-n+1)，u(k)，…，u(k-m+1)]^T (2.53)

而PE的权系数向量为w(k)

w(k)＝[w₁(k)，w₂(k)，…，w_n(k)，w_n+1(k)，…，w_{n+
m}(k)]^T (2.54)

由于对象仿真器PE是由线性神经网络构成，其输出y由下式求出

	(2.55)
在实时训练中，权系数采用Widrow-Hoff规则进行更新，即
	(2.56)

其中：α∈(0，2)，是衰减因子：

E是接近于0的小数，用于防止在x^T(k)x(k)等于0时分母为0；

e(k+1)是输出偏差，e(k+1)＝y(k+1)-y_E(k+1)。

利用式(2．56)进行学习训练，最终目的就是使输出偏差e(k+1)最小化。而且，当e(k+1)——U时，从式(2．56)看出有w(k+1)＝w(k)。

2．神经控制器NC

神经控制器NC也是二层神经网络构成，输入端有n+m个，输出端有一个。它的结构如图2—18所示。输入为z(k)，输出为控制量u(k)。

在k时刻，NC的输入为z(k)．有

z(k)＝[z₁(k)，z₂(k)，…，z_n+1(k)，z_n+2(k)，…，z_n+m(k)]^T
=[r(k+1)，-x₁(k)，…，-x_n(k)，-x_n+2(k)，…，x_n+m(k)]^T
=[r(k+1)，y(k)…，y(k-n+2)，-u(k-1)，…，-u(k-m+1)]^T (2.57)

注意在式(2．57)中没有-Xn+1(k)，即y(k-n-1)这项。

神经控制器NC的权系数向量为W'(k)有

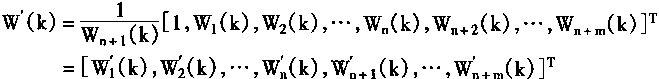	(2.58)
显然．NC的权系数向量w’(k)是PE的权系数向量W(k)的函数。由NC产生的控制输出信号u(k)，由下式求出：
	(2.59)

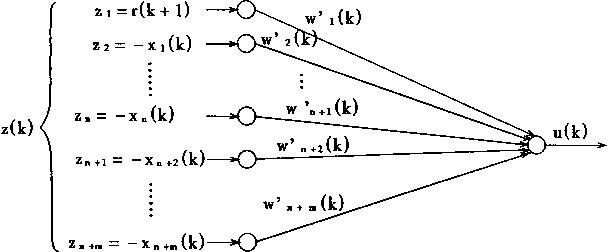
图2-18 神经控制器NC的结构

3．控制系统的信息处理过程

在图2—16所示的神经网络控制系统中，信息的处理过程和步骤如下：

(1)取给定值r(k+1)，取对象输出值y(k)。

(2)用原有权系数向量W(k-1)，通过式(2．55)计算对象仿真器PE的预测输出y_E(k)

(3)计算偏差e(k)＝y(k)—y_E(k)，并且利用式(2．56)计算出新的权系数向量W(k)。

(4)用式(2．58)更新神经控制器NC的权系数向量w'(k)。

(5)神经控制器Nc通过式(2．59)产生控制量u(k)。

三、控制系统的闭环性能分析

在确立闭环系统的性能之前先考虑对象仿真器的一些性质。

设W₀是对象仿真器PE训练之后得到的最终权系数向量

W₀=[W₀₁,W₀₂,...,W_0n+m]^T (2.60)

则W₀满足下式

(2.61)

也即是说在权系数为W₀向量时，PE能精确预测对象的输出。

引理：由式(2．53)—(2．55)所表述的对象仿真器PE，满足如下性质：

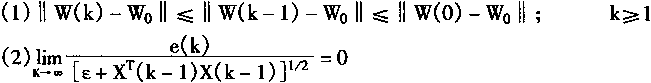
证明：

考虑权系数误差ΔW(k)

ΔW(k)=W(K)-W₀ (2.62)

根据式(2．55)，(2．6I)，(2．62)，则系统输出误差e(k)可以表达为权系数误差ΔW的函数，即

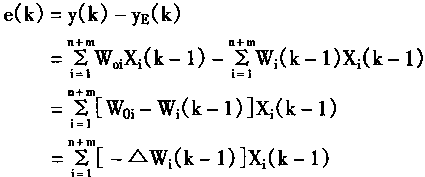
=-X^T(k-1)ΔW(k-1) (2.63)

把式(2．56)两边减去W₀，可求出权系数误差，则得：

	(2.64)
把上式(2．64)两边平方有

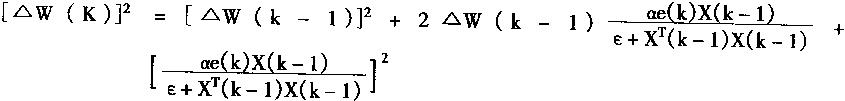(2.65)

从式(2.63)可知

e(k)=-X^T(k-1)ΔW(k-1)

即有

代入式(2.65)，有

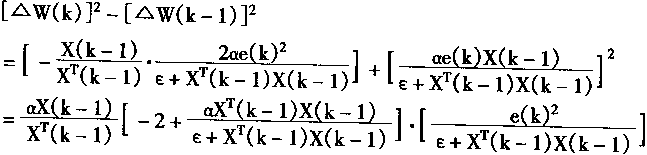(2.66)

从式(2.66)中，有

α∈(O，2)，故即α＞0；

X(k-1)/XT(k-1)，XT(k-1)X(k-1)都为正；

e(k)2也必定大于0，ε是趋于0的正数。

所以，在式(2.66)中

(2.67)

的结果确定了[ΔW(k)]²-[ΔW(k-1)]²的正负。

令 H=x^T(k-1)x(k-1)

则式(2.67)可写为：

则有

从而可知

最后有

[ΔW(k)]²-[ΔW(k-1)]²<0 (2.68)

式(2．68)说明引理的性质(1)成立。

根据性质(1)，则当k——∞，则有w(k)＝W₀．故而在式(2．66)中两边都为0。这也就是必定有

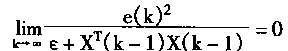(2.69)

可见，引理的性质(2)成立。

证毕。

有了上面的引理，就可以给出由式(2．53)—(2．59)组成的控制结构对对象式(2．52)执行适应控制的闭环性质定理。

定理：在对象由式(2．52)描述的控制中，式(2．53)—(2．59)构成的适应控制有如下的闭环性质：

(1)输入信号u(t)，输出信号y(t)都是有界的。

证明：

设系统的跟踪误差用e'(k)表示

e'(k)=y(k)-r(k) (2.70)

y(k)由式(2．61)给出。

r(k)可由式(2．57)，(2．58)，(2．59)求出，先用W_n+1(k)乘〔2．59)两边，则有

W_n+1(k-1)u(k-1)=r(k)+W₁(k-1)(-X₁(k-1))+.....,+W_n(k-1)(-X_n(k-1))+W_n+2(k-1)(-X_n+2(k-1))+......,Wn+m(k-1)(-Xn+m(k-1))

整理后有

r(k)=W₁(k-1)X₁(k-1)+......,+W_n(k-1)X_n(k-1)+W_n+1(k-1)u(k-1)+W_n+2(k-1)X_n+2(k-1)+......,+W_n+m(k-1)X_n+m(k-1)

(2.71)

由于 u(k-1)=Xn+1(k-1)

故而有

	(2.72)
从式(2.61)和式(2.72)，则有
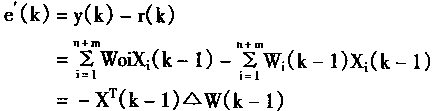	(2.73)
从引理的性质(2)有
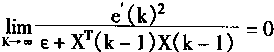	(2.74)

只要证明x^T(k-1)x(k-1)是有界的，就可以证明e(∞)＝0，也就可以证明定理中的性质(2)。

下面证明‖x(k-1)‖有限。

从对象式(2．52)有关条件，对象的输入输出信号满足

(2.75)

其中：1≤i≤k；m₁<∞；m₂<∞。

根据式(2．52)对象的满足条件，从式(2．53)则有

	(2.76)
既然，给定信号r是有界的，所以跟踪误差有
	(2.77)

从而有|e'(k)|+m3≥|y(k)|

由此，式(2．76)可以写为：

(2.78)

其中：0≤C₁≤∞；0≤C₂≤∞。

假设跟踪误差e'(k)有界，则从式(2．78)可知：‖x(k)‖同样有界；这样从式(2．74)可知

	(2.79)
显然，定理的性质(2)成立。假设跟踪误差e'(k)无界，则存在时刻序列\|kn\|，令
	(2.80)

取m4＝max(1，ε)

考虑

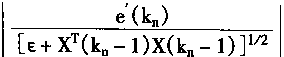
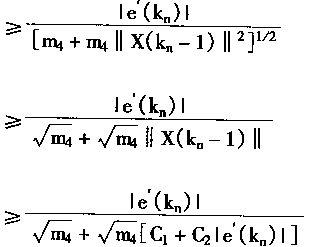	(2.81)
对式(2.81)取极限有
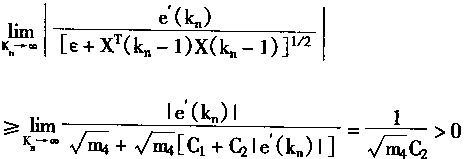	(2.82)

这个极限存在说明e'(K)有界，假设其无界不成立。

由于e'(k)有界，故式(2．79)是必定成立的。由于e'(k)＝y(k)-r(k),而r(k)有界,所以，y(k)有界。从式(2．75)可知u(k)也有界。则定理的两个性质成立。

证毕。

四、系统实际运行情况

当对象的结构不同时，可以用于检验图2-16所示的神经适应控制系统的运行结果。对象仿真器PE，神经控制器NC分别由式(2.52)-(2.55)和式(2.57)-(2.59)所描述；学习时采用式(2．56)和式(2．58)。

1．对有噪声的稳定对象的控制

对象由下式表示

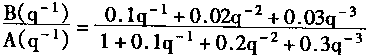
设对象仿真器PE和神经控制器NC输入的向量为6个元素，有n＝m＝3。在训练学习时PE的权系数向量更新取α和ε的值如下：

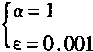
权系数向量的初始值取

W(0)=[0,0,0,1,0,0]^T

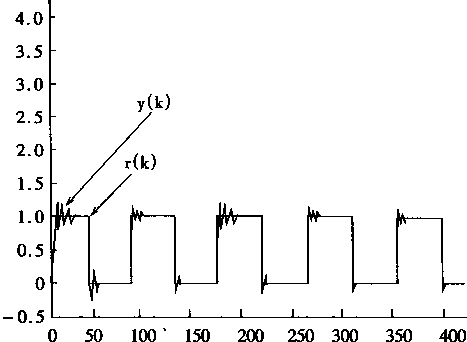
图2-19 给定值r和对象输出y

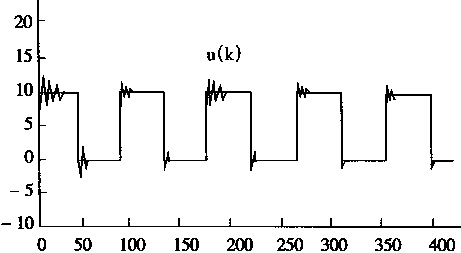
图2-20 NC产生的控制信号u

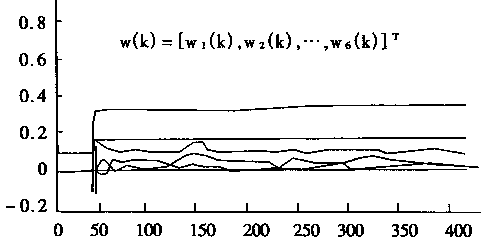
图2-21 PE的学习过程W(k)的变化

噪声是平均值为零的高斯白噪声。

给定输入r是幅值为1的方波；每方波周期采样80次。

控制结果和情况如图2—19和图2—20所示。其中图2—19是对象输出和给定值的情况；图2—20是NC产生的控制信号u(k)。
很明显，对象仿真器能正确地预测对象的动态过程。

图2—21给出了对象仿真器PE的学习过程。

2．对不稳定对象的控制

不稳定对象由下式表示

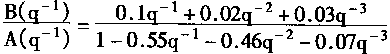
在系统中，PE和NC的输入都采用6个元素的向量，故n＝m＝3。在训练学习时．PE权系数向量更新取α和ε的值为

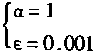
权系数向量初始化取值为

W(0)=[0,0,0,1,0,0]^T

给定输入r为幅度为1的方波，方波每周期采样80次。

控制情况和结果以及邢学习时的w(k)变化情况分别如图2—22，图2—23，图2—24所示。对于不稳定对象，显然在过渡过程中有较大的超调；但在PE学习之后，对象输出能跟踪给定r。

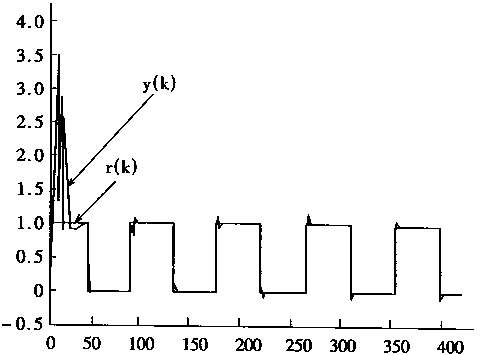
图2-22 给定r和对象输出y的波形

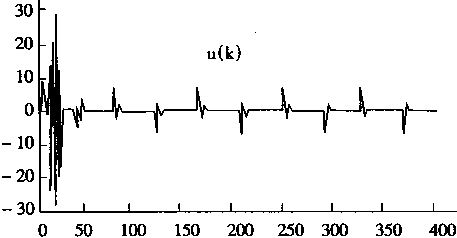
图2-23 NC产生的控制信号U的波形

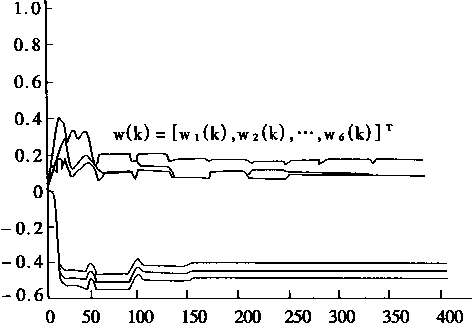
图2-24 PE学习时W(k)的变化情况