2.3.2 水温神经网络控制系统
温度控制是人们在工业.家庭生活等各个领域经常遇到的控制系统。水温控制是温度控制的一种类型。采用神经网络对水温控制是一种新的控制方式和控制手段。在这个水温控制系统中,神经网络的训练采取第2.2节神经网络控制器与学习中所介绍的联机学习方法与算法。
一、温度控制系统的模型
对一个连续温度控制系统,可以用下面数学表达式来描述
| (2.83) |
其中:t是时间;
y(t)是输出温度;
f(t)是加给系统的热量;
Yo是室温,一胶为常数;
c是系统的热容量;
R是系统边界与周围的热阻。
假定在式(2—83)中,RC是常数,从阶跃响应准则可以得到其对应的离散系统脉冲传递函数的表达式:
| (2.84) | |
| 其中:u(k)为系统输人;
y(k)为系统输出; Ts为采样周期; a(Ts)和b(T8)由下式决定: |
|
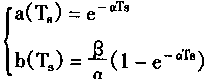 |
(2.85) |
在式(2.85)中。α,β是由R,C确定的常数。
在一般温度控制中,输出温度不允许超过一定的极限值,也即是(2.83)所描述的系统具有饱和的非线性特性。故控制对象可以表达为:
| (2.86) |
对于一个具体的系统,有
α=1.00151*10-4 β=8.67973*10-3
r=40.0 Yo=25.0℃
0≤u(k)≤5 Ts>10S
这是一个实际水缸对象得到的有关参数。
把式(2.15)和式(2.86)作比较;显然有p=1,Q=0。根据所选择的参数,系统是一个水缸的单输入单输出温度控制系统;这个系统在室温到70℃之间呈现出线性特性,而再升到80℃左右则变成非线性同时达到饱和。
二、水缸温度控制系统和神经网络结构
水缸温度控制系统的结构如图2—25所示,它由水缸,计算机,接口部件,检测器,功率控制部件和加热器组成。
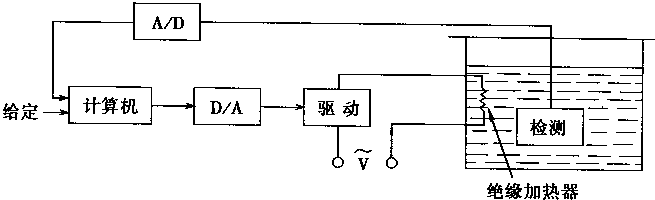
图2-25 水缸温度控制系统结构
给定信号输入计算机作为控制的期望信号。计算机通过A/D转换等接口部件接收温度检测器所检测的结果,在计算机内部以软件算法执行学习以及神经网络的处理,产生控制信号去控制功率驱动部件,再使加热器以恰当的功率加热;加热器以PWM方式执行功率调节。
温度检测器为半导体温度传感器件,A/D转换器为8位,计算机产生的控制信号在0—5V之间,它用于产生PWM的脉宽,加热器功率为1.3KW,水缸是一个含7升水的小水缸。
考虑神经网络组成的对象仿真器PE和神经控制器NC都用4层的多层神经网络组成。通过式(2.86)可知,神经网络有两个输入,一个为y(k),一个为u(k)。这两个输入都归一化到-1和+1之间。每个隐层含有6个传递函数为s函数的神经元。而输出层则是一个线性神经元。所以,PE和NC的结构如图2—26中所示
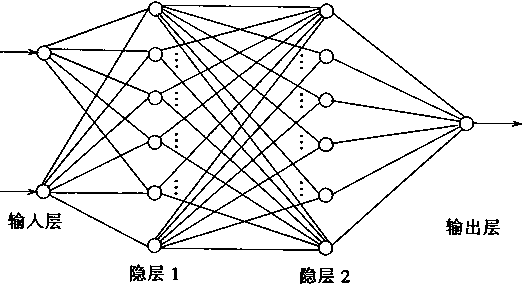
图2-26 PE和NC的结构
在计算机中.神经网络控制器是通过软件算法实现的。在整个系统中,神经网络控制器和对象仿真器的位置和作用如图2—27中所示。从图中可以看出对象仿真器PE的输入是u(k)和y(k),而输出只有一个yE;神经控制器NC也有两个输入,分别为r(k+1)和u(k-1),而输出则是u(k)。很明显,这是一种间接适应控制结构,采用这种结构有利于对水缸的特性进行学习。
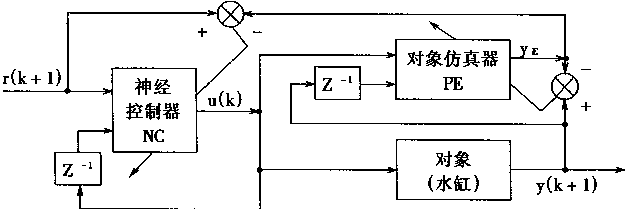
图2-27 系统的神经网络控制结构
对于图2—26所示的对象仿真器邢和神经网络控制器NC,在实时学习时采用下面规则对权系数进行修改,即
| (2.87) | |
| 也即是新的权系数Wn+1为 | |
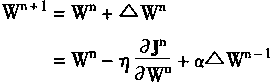 |
(2.88) |
其中:n是训练学习次数序号:
w是权系数;
η是学习速率;η>O;
u>0,是修正系数;
J是误差函数。
在对PE和NC执行实时学习之前,首先对PE进行脱机的粗训练。对PE的脱机训练是以对对象的阶跃响应试验或脉冲响应试验所纪录的数据为依据的。为了得到对象的输入输出数据,把脉冲加到对象的输入端,同时把对象的输入输出数据纪录下来。为了复盖控制空间的相关的范围,在所纪录的数据对中选择10对能代表控制范围的数据。为了使控制效果有一定的裕废,最小和最大的数据应比实际控制范围要宽一些。
在PE通过脱机训练之后,可以得出了其初步的权系数;对于NC则随机赋于小的权系数,以避免传递函数为s函数的神经元饱和。在这样初始条件下,则可以对系统执行实时运行和学习。
三、实际控制过程及结果
对于实际水缸的水温控制系统,它的控制给定曲线是一条阶梯温度曲线;这条给定的温度曲线为:
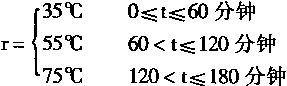
它的图形如图2-28所示。
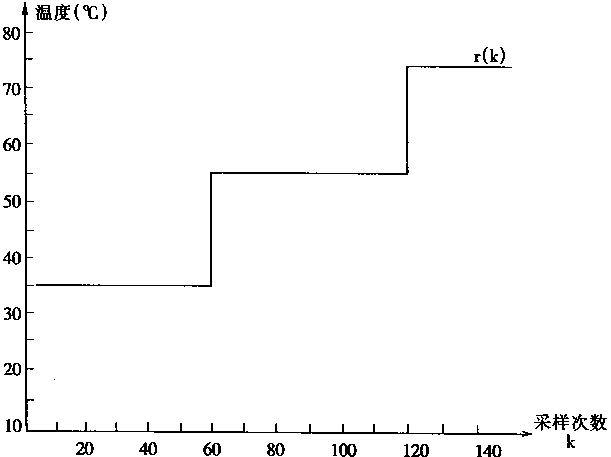
图2-28 给定温度曲线
在系统实际运行时,由于水温升高是较为缓慢的,所以对水温的采样周期选择为30秒。这种采样周期合符水缸水温控制的实际情况。
在每个采样周期,对象仿真器PE更新15次,神经控制器NC执行11个学习周期。在神经控制器的11个学习周期中,有10个周期采用有关的多次学习逼近,有1个周期采用间接适应控制的学习方法。这些学习方法在2.2节中的联机学习方法及算法已进行了介绍。
在最初的10次试验中,神经控制器NC在每个采样周期中的多次学习逼近采用的是预测输出误差逼近;也即是说,在每个采样周期中有10个预测输出误差逼近学习周期,1个间接适应控制学习周期。
在随后的各次试验中,则在每个采样周期中,用5个直接逆控制误差逼近学习周期和5个预测输出误差逼近学习周期。
在神经网络实时学习中,学习参数选择如下:
学习速率η=0.1;
修正系数α=0.2;
学习时的偏差函数采用误差平方函数,形式如式(2.41)所示。
通过34次实时试验,神经网络在实时学习中确定了权系数,则用这些权系数所最终描述的神经网络PE和NC对系统执行控制,可得出如图2—29所示的控制效果。
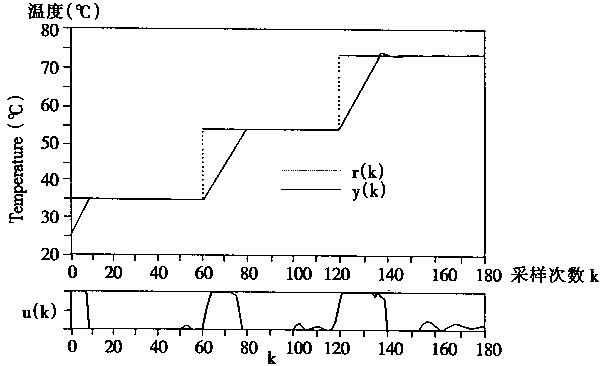
图2-29 34次试验后所得的控制效果
在图2—29中,上图是给定温度曲线r(k)和控制结果曲线y(k)的变化情况。在给定温度以阶跃形式从室温升到35℃时,大约经过10个采样周期,系统输出会很好地跟踪给定35℃的温度。这时因为室温的温度大约为25℃。当给定温度从35℃阶跃上升到55℃时,大约经过18个采样周期,输出能很好地跟踪给定的55℃,而当给定温度从55℃再以阶跃形式上升到75℃时,大约经过四个采样周期后输出能跟踪给定的最终温度75℃。这种特性和水缸的特性有关,因为越接近80℃,水缸的非线性特性越明显。总的控制情况说明:通过实时学习的神经网络对象仿真器PE和神经网络控制器NC能满意地实现对水缸水温的控制。
在图2—29中,下因给出的是神经控制器Nc的输出控制信号;很明显,在采样周期次数序号为k=0—10时,NC的输出u(k)是一幅值为5的方波;而在采样序号k=60—78时.PE输出u(k)是一幅值为5而宽度为9分钟的方波;而在k=120—140时,NC输出U(k)是幅值为5同时宽度为10分钟的方波。
当空温为20℃,而控制给定温度曲线由下式给出:
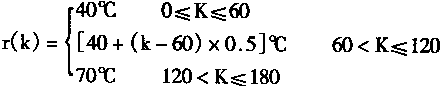
则控制的情况如图2—30所示。
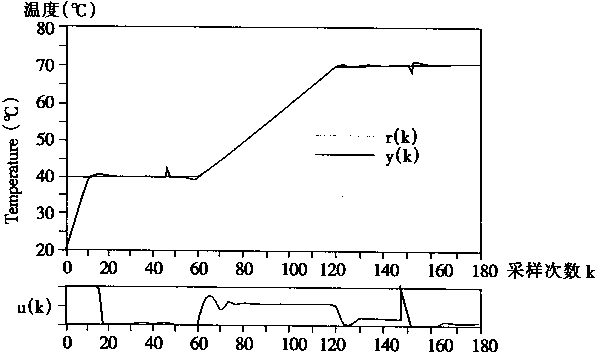
图2—30 阶跃及匀速给定的响应情况
在图2—30中,上图是系统的给定温度曲线r(k)以及系统的输出温度曲线的响应情况,从图中看出系统有良好的响应特性,特别是匀速给定的上升温度曲线,即在60<K≤120时有很好的跟踪能力。在图中,当k=50时,人为加入+5℃的干扰;而在k=150℃时,加入人为的-5℃干扰;而情况表明控制系统有很快的适应能力。图2—30的下图则是神经控制器Nc的输出控制信号U(k)的波形。