回目录     上一页         下一页

第三章 模糊神经网络

模糊逻辑和神经网络的发展使到近十年以来智能控制得到十分重要的进展；由于模糊逻辑和神经网络又是两个截然不同的领域；它们的基础理论相差较远。但是，它们都是智能的仿真方法。是否可以把它们结合起来而加以应用呢?从客观实践和理论的溶合上讲是完全可以令它们结合的。把模糊逻辑和神经网络相结合就产生了—种新的技术领域：这就是模糊神经网络。模糊神经网络是正在不断探讨和研究的一个新领域。在目前，模糊神经网络有如下三种形式：

1．逻辑模糊神经网络

2．算术模糊神经网络

3．混合模糊神经网络

模糊神经网络就是具有模糊权系数或者输入信号是模糊量的神经网络。上面三种形式的模糊神经网络中所执行的运算方法不同。

模糊神经网络无论作为逼近器，还是模式存储器，都是需要学习和优化权系数的。学习算法是模糊神经网络优化权系数的关键。对于逻辑模糊神经网络，可采用基于误差的学习算法，也即是监视学习算法。对于算术模糊神经网络，则有模糊BP算法，遗传算法等。对于混合模糊神经网络，目前尚未有合理的算法；不过，混合模糊神经网络一般是用于计算而不是用于学习的，它不必一定学习。
模糊神经网络可用于模糊回归、模糊控制器、模糊专家系统、模糊谱系分析、模糊矩阵方程、通用逼近器。

在控制领域中，所关心的是由模糊神经网络构成的模糊控制器。在这一章中．介绍模糊神经网络的基本结构、遗传算法、模糊神经网络的学习算法，以及模糊神经网络的应用。

3．1 模糊神经网络概念和结构

模糊神经网络是一种新型的神经网络，它是在网络中引入模糊算法或模糊权系数的神经网络。模糊神经网络的特点在于把模糊逻辑方法和神经网络方法结合在一起。

对于模糊神经网络而言，最重要的有如下三点：

第一，模糊神经元模型的开发；

第二，模糊权系数模型的开发；

第三．模糊神经网络学习算法的开发。

1974年，S.C.Lee以和E.T.Lee在Cybernetics杂志上发表了“”Fuzzy sets and neural networks”一文，首次把模糊集和神经网络联系在一起；接着，在1975年，他们又在Math.Biosci杂志上发表厂“Fuzzy neural networks”一文，明确地对模糊神经网络进行了研究。在文章中，作者用0和1之间的中间值推广了McCulloch-Pitts神经网络模型。在以后一段时间中，由于神经网络的研究仍处于低潮，所以在这方面的研究没有取得什么进展。1985年，J.M Keller和D.Huut提出f把模糊隶属函数和感知器算法相结合。1989年T．Yamakawa提出了初始的模糊神经元．这种模糊神经元具有模糊权系数，但输入信号是实数。1992年，T．Yamakawa又提出了新的模糊神经元，新的模糊神经元的每个输入端不是具有单一的权系数，而是模糊权系数和实权系数串联的集合。同年，K.Nakamura和M.Tokunaga分别也提出了和T．Yamakawa的新模糊神经元类同的模糊神经元。1992年，D.Nauck和R.Kruse提出用单一模糊权系数的模糊神经元进行模糊控制及过程学习。而在这一年，I.Requena和M.Delgado提出了具有实数权系数，模糊阀值和模糊输入的模糊神经元。1990年到1992年期间，M．M．Gupta提出了多种模糊神经元模型，这些模型中有类同上面的模糊神经元模型．还有含模糊权系数并可以输入模糊量的模糊神经元。1992年开始，J．J．Backley发表了多篇关于混合模糊神经网络的文章，它们也反映了人们近年来的兴趣点。

在下面分别对模物神经网络的不同结构形式进行介绍。这些结构包括逻辑模糊神经网络、算术模糊神经网络、混合模糊神经网络、其他模糊神经网络。

3.1.1 逻辑模糊神经网络

逻辑模糊神经网络是由逻辑模糊神经元组成的。逻辑模糊神经元是具有模糊权系数，并且可对输入的模糊信号执行逻辑操作的神经元。模糊神经元所执行的模糊运算有逻辑运算、算水运算和其它运算。无论如何，模糊神经元的基础是传统神经元。它们可从传统神经元推导出。

可执行模物运算的模糊神经网络是从一般神经网络发展而得到的。对于一般神经网络．它的基本单元是传统神经元。传统神经元的模型是由下式描述的：

	(3-1)
当阀值θi=0 时，有
	(3-2)

其中：X_j是神经元的输入；

W_ij是权系数；

f[·]是非线性激发函数；

Y_i是神经元的输出。

如果把式(3—2)中的有关运算改为模糊运算，从而可以得到基于模糊运算的模糊神经元，这种神经元的模型可以用下面式(3—3)表示：

	(3-3)
其中：⊕表示模糊加运算； ⊙表示模糊乘运算。 同理，式(3—3)中的运算也可以用模糊逻辑运算取代。从而有“或”神经元：
	(3-4)
或者表示为：
	(3-5)
同理也就有“与”神经元的模型如下：
	(3-6)
或者表示为：
	(3-7)

下面专门考虑基于模糊逻辑运算的模糊神经网络的有关特性。

一、网络的模型

对于一个神经元，考虑其输入信号是以隶属函数表示，而不是以绝对值表示，则把输人向量表示为：

(3-8)

很明显，这些输入信号是在(n+1)维超立方体[0,1]ⁿ⁺¹之内，隶属函数的隶属度为[0，1]间的值，而输入信号是隶属函数，也即是以论域元素及其隶属度表示，故在式(3-8)中，X_n(t)是模糊量。

同理，网络中的权系数向量也可用起立方体[0，1]ⁿ⁺¹中的信号表示：

(3-9)

在式(3-9)中，权系数W_n(t)模糊量，这时的神经元结构如图3-1所示。

对于输入X1,X2[0,1]，定义AND操作为T映射：

T:[0,1]*[0,1]——[0,1]

即

	(3-10)
同理，定义OR操作为S映射 S:[0,1]*[0,1]——[0,1] 即
	(3-11)

并且，定义N操作为N映射：

N:[0,1]——[0,1]

即

Y_N=N[X₁]=1-X₁              (3-12)

故而有 N(0)=1，N(1)＝0，NN(x)＝X

对于T，S算子，则有如下重要性质：

T(0，0)＝0 S(0，0)＝0

T(1，1)＝1 S(1，1)=1

T(1，X)＝X S(0，X)＝X

T(X，Y)＝T(Y，X) S(X，Y)＝S(Y，X)

同时，根据Morgan定理，则有如下关系：

T(X1，X2)＝1-S(1-X1，1-X2)

S(X1，X2)＝1-T(1-X1，1-X2)

在基于模糊逻辑操作的模糊神经网络中，神经网络的输入和权系数向量有：

X(t)∈[0,1]ⁿ⁺¹

W(t)∈[0,1]ⁿ⁺¹

则在神经网络模型(3—2)中，权系数和输入信号的乘操作用T操作取代，求和操作由s操作取代，则有：

(3-13)

其中：f|·|是非线性函数。

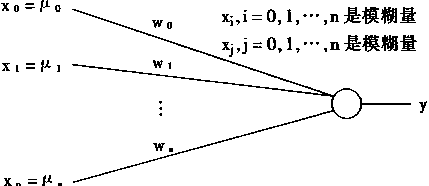
图3-1 模糊神经元模型

二、单极到双极的变换

上面的模糊逻辑操作是定义在[0，1]正区间内的；所以，神经网络的状态也就局限于[0，1]正区间内。为了考虑神经网络的激发和抑制特性，需要考虑神经网络的正和负的输入向量。所以，神经网络的输人和权系数取[-1，1]区间的值。

为了说明在[-1，1]区间的逻辑操作，故按照先前[0，1]区间的单极性情况，再转换到新的[-1，1]区间的双极性情况中，则随后就可以定义在[-1，1]区间的有关逻辑操作。

考虑单极信号X(t)∈[0，1]，则对应双极信号Z(t)∈[-1，1]定义为：

Z(t)=2X(t)-1          (3-14)

同理，N[Z]定义为：

N[Z]=-Z(t)            (3-15)

用式(3—14)可以把在[0，1]区间定义的S，T操作转换成在[-1，1]区间的操作。

在[-1，1]区间的T(AND)，S(OR)操作性质如下：

T(-1,-1)=-1           S(-1,-1)=-1

T(1，1)=1 S(1，1)＝1

T(1，Z)＝Z S(-1，Z)＝Z

T(Z₁，Z₂)＝T(Z₂，Z₁) S(Z₁，Z₂)＝S(Z₂，Z₁)

在[-1，1]区间，T，S的Morgan定理为

T(Z₁，Z₂)=-S(-Z₁，-Z₂)

S(Z₁，Z₂)＝-T(-Z₁，-Z₂)

利用变换式(3—14)可以把n+1维向量x(t)∈[0，1]ⁿ⁺¹转换成n+1维向量Z(t)∈[-1，1]ⁿ⁺¹。这时，神经元的操作和输出可以表示如下：

Y=f[u]∈[-1,1]              (3-16)

其中：

上式(3-16)也可以写成：

或

或

在式(3—16)中f[·]的定义如下

f[u(t)]=|u(t)|^g·sgn[u(t)], g>0            (3-17)

其中：g是增益参数，它用于控制S函数的激发水平。

3．1．2 算术模糊神经网络

算术模糊神经网络是可以对输入模糊信号执行模糊算术运算，并含有模糊权系数的神经网络。通常，算术模糊神经网络也称为常规模糊神经网络，或称标推模糊神经网络。

常规模糊神经网络一般简称为RFNN(Regular Fuzzy Neural Net)或称为FNN(Fuzzy Neural Net)。在一般情况下，都把常规模糊神经网络简称为FNN。

常规模糊神经网络有三种基本类型，并分别用FNN1，FNN2，FNN3表示。这三种类型的意义如下：

1．FNN1是含有模糊权系数，而输入信号为实数的网络。

2．FNN2是含有实数权系数，而输入信号为模糊数的网络。

3．FNN3是含有模糊权系数，而输入信号为模糊数的网络。

下面先对模糊算术运算的定义进行介绍，随后说明常规模糊神经网络的结构和性质。

一、模糊算术运算

模糊算术运算包括有模糊乘和模糊加两种基本运算，它们的定义分别说明如下：

1．模糊乘

设N，M是两个模糊集，它们的隶属函数分别为：

则N和M的模糊乘用下式表示：

	(3-18)
其中：符号⊙表示模糊乘运算。 模糊乘P的隶属函数由下式给出：
	(3-19)
即
	(3-20)

式(3—19)，(3—20)定义了基于扩张原理的模糊乘运算。模糊乘的意义如图3—2所示。

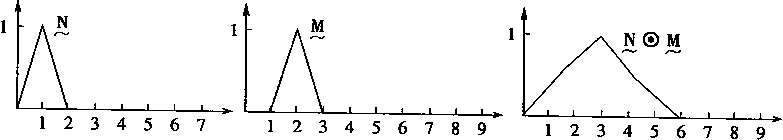
图3-2 模糊乘

2．模糊加

设N，M是两个模糊集，它们的隶属函数分别为：

则N和M模糊加用下式表示

	(3-21)
其中：符号⊕表示模糊加运算。 模糊和H的隶属函数由下式给出：
	(3-22)
或
	(3-23)

式(3—22)，(3—23)定义了基于扩张原理的模糊加运算。模糊加的意义如图3—3所示。

图3-3 模糊加

3．非线性映射

设N是一个模糊集，f[·]是非线性映射，则N的非线性映射定义如下

非线性映射结果G的隶属溺数由下式给出

	(3-24)
或
	(3-25)

一般，在神经网络中的激发函数也称传递函数；传递函数通常采用S函数，即有f(x)＝1/[1+exp(-X)]故而，模糊神经网络中模糊量的非线性映射就是S函数；并用f[·]表示。式(3—24)，(3—25)定义基于扩张原理的非线性映射。它的意义如图3—4所示。

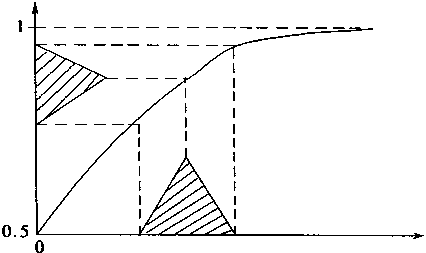
图3-4 非线性映射

常规模糊神经网络最典型的结构是FNN3型结构，而FNN1，FNN2型结构和FNN3相同；其运算过程都可以从FNN3型结构及运算过程中推出。在FNN3中，权系数和输入信号都是模糊数，而神经元对信息的处理采用模糊加、模糊乘和非线性的S函数。

典型的FNN3的结构如图3—5所示。它是一个三层神经网络，有含2个神经元的输入层，含2个神经元的隐层和含1个神经元的输出层。网络中的神经元分别用编号1—5标出。

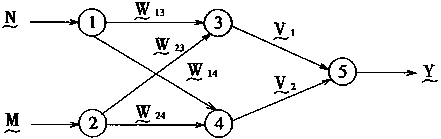
图3-5 算术模糊神经网络

很明显，对神经元3．它的输人为U₃：

	(3-25)
对于神经元4，其输入为U4：
	(3-26)
用O3，O4分别表示神经元3，4的输出，则有
	(3-27)
对于神经元5，其输入为U5，输出为Y，则有
	(3-28)
	(3-29)

最后的输出Y，是由传递函数S函数求出的，故模糊数YE[0，1]。

对于模糊神经网络，在输入为N，M时其输出为Y；则可以看作N，M通过神经网络后映射为Y，并表示为：

(3-30)

三、常规模糊神经网络的性质

用L表示所有实模糊数的集合；而Lx L用Ω表示，称为2维模糊数空间。

设N，M∈L，Y∈L，则从Ω到L的映射F：Ω——L，可表示为

(3-31)

当并且仅当

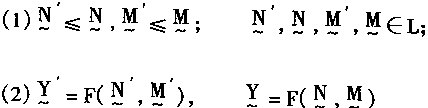
则有

则称映射f：Ω——L是单调的。

考虑图3—5所示的模糊神经网络，并用FNN表示，则有映射

如果在图3—5中输入的信号是N'，M'，并且有

	(3-32)
	(3-33)
令
	(3-34)
则有
	(3-35)
令
	(3-36)
则有
	(3-37)
从而有
	(3-38)
	(3-39)
令
	(3-40)
则有
	(3-41)
最后利用扩张原理和S函数f(x)＝(1+e-x)-1计算输出
	(3-42)
	(3-43)
隶属函数分别为：
	(3-44)
	(3-45)
由于
，故
	(3-46)

很明显，对于图3—5所示的模糊神经网络，它是一个单调的网络。

实际上，可以把上述情况扩展到一级的常规模糊神经网络。最后有如下结论：

对于一个模糊神经网络，如果它的算术运算是基于扩张原则的，则这个模糊神经网络是—个单调的网络。即

则有

从上面的结论可知：对于任何从o到L的连续单调映射，都可以用基于扩张原理的常规模糊神经网络进行逼近。反之，如果映射是非单调的，则不能用常规模糊神经网络进行逼近。

3．1．3混合模糊神经网络

混合模糊神经网络简称HFNN(Hybrid Fuzzy Neural Net)。在网络的拓扑结构上，混合模糊神经网络和常规模糊神经网络是一样的。它们之间的不同仅在于如下两点功能：

1．输入到神经元的数据聚合方法不同；

2．神经元的激发函数，即传递函数不同。

在混合模糊神经网络中，任何操作都可以用于聚合数据，任何函数都可以用作传递函数去产生网络的输出。对于专门的应用用途，可选择与之相关而有效的聚合运算和传递函数。而在常规模糊神经网络，也即标准模糊神经网络中，数据的聚合方法采用模糊加或乘运算，传递函数采用S函数。

下面就以具体的混合模糊神经网络来说明它的网络操作情况；然后再介绍这种网络的性质。

一、混台模糊神经网络的操作

为了具体说明在混合模糊神经网络的操作过程，首先考虑图3—6所示的网络拓扑结构。在这个网络中各个神经元的聚合运算和传递函数可以是不同的。正是因为它不象常规模糊神经网络那样采用标准的加、乘运算以及s函数，而是可随意在任何层任何神经元采用不同的操作，所以，它被称为混合(Hybrid)模糊神经网络。

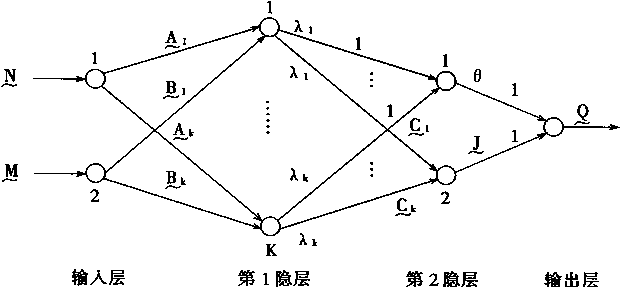
图3-6 混合模糊神经网络

1．输入层和第1院层的工作情况

在第1隐层中一共有K个神经元，在输入层中有2个节点和第1隐层的一个神经元连接；也即是说，第1隐层的每个神经元有2个输入端。

设L是所有实模糊数的集合，在图3—6中，N、M、Ak、Bk、Ck、Q、J是实模捌数。用E表示两个模糊效之间相等的程度测量，并且在N＝M时，有

则在第1隐层的第k个神经元的输入用I_1k表示，有

(3-47)

其中．A_k，B_k是权系数1<k<K_c。

很明显，在混合模糊神经元中，输入信号N，M和权系数A_k，B_k之间的交互作用是用测度E(N，A_k)，E(M，B_k)来量度的，最后求出它的最大值为结果输入。

在混合模糊神经网络第1隐层中，传递函数f为阶跃函数，并且有输出λ_k

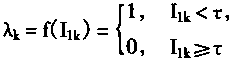(3-48)

其中：t为神经网络的阀值，t>0；1≤k≤K。

在这里，第1隐层的所有神经元的传递函数相同，阀值相同。

2．第2隐层的工作情况

在第2隐层中．第1个神经元的权系数为1。从图3—6中看出，输入第2隐层第1个神经元的输入数据为I₂₁，即有

	(3-49)
由于λk是实数0或1，故I21是精确值。 该神经元的传递函数采用相同函数，故有
f(X)=X	(3-50)
故而，这个神经元的输出θ等于其输入I21，即
θ=I21	(3-51)

对于第2隐层第2个神经元，它的权系数分别为C1，C2．…，Ck。所以，其输入表示为I₂₂．并有

	(3-52)
并且λk，Ck的取值如下
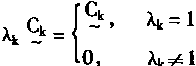	(3-53)
同时，式(3—52)中的符号Σ是模糊加的标准操作，其意义由式(3—22)，(3—23)给出。 这个神经元的传递函数也采用相同函数，故而有输出J，
	(3-54)

3．输出层的工作情况

在输出层中，权系数为10但是输出层神经元的聚合操作是除法；所以．输出神经元的输人数据为I

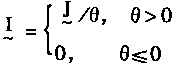(3-55)

传递函数也采用相同函数，所以输出等于输人，即有

从上面分析可以知道，图3—6所示的混合模糊神经网络的最后输出P可表示为

	(3-56)
当在λk＝1时，则有
	(3-57)

二、混合模糊神经网络的性质

混合模糊神经网络由于它所采用的运算和常规模糊神经网络不同；所以，它有独特的性质。如果用F表示图3—6所示的由相等测量E，阀值t，权系数Ak，Bk，Ck所构造的混合模糊神经网络；那么，F是一个通用逼近器。
换而言之，图3—6所示的混合模糊神经网络可以逼近任意的双输入单输出模糊函数。

1.基本定义和概念

L表示所有实模糊数的集合；则Ω表示2维实模糊数集合，即 Ω＝LxL。

定义1：模糊数N、M的。截集用N(α)，M(α)表示，则有

其中，n1(α)是。截集N(α)的下界元素，n2(α)是N(α)的上界元素；m1(α)是M(α)的下界元素，m2(α)是M(α)的上界元素。

模糊数N，M的Hausdorff心13测度由下式给出：

	(3-58)
定义2：在集合L中，模糊数N，M之间的距离用d表示，并由下式给出
	(3-59)

定义3：在2维实模糊数集合Ω＝L xL中，两个2维模糊数(N1，M1)和(N2，M2)之间的距离用D表示，并且由下式给出：

(3-60)

定义4：F是连续映射

F：Ω——L

其中：N，M是L的模掘数，Y也是L中的模糊数。

2．通用逼近器定理

定理：图3—6中由E，t，Ak，Bk，Ck所构造的模糊神经网络F是一个通用逼近器。

证明：

设u是Ω中的紧子集，F是U到L的连续映射，HFNN是由Ak，Bk，Ck，E，t所定义的空间F中的混合模糊神经网络。

对于模糊数N，M，有映射

		(3-61)
同时，把N，M输入混合模糊神经网络HFNN，有输出：
		(3-62)
存在无穷小的数ε>0，如果对于U中的所有(N，M)都有
		(3-63)
		(3-64)
其中：D是距离，如式(3—59)所示。 则说明HFNN可以逼近映射F；也即是说F是一个通用逼近器。 下面给出证明过程： (1)设对于给定ε>0，令
		(3-65)
则对应存在δ>o，令
		(3-66)
其中：D(N1．M1)，(N2，M2)属于U。 对U中的每一个(N，M)，令
		(3-67)
这即是紧集合U的开复盖(open cover)。因此，存在有限子复盖(subcover):
		(3-68)
令Nk＝Ak，Mk＝Bk，以及映射F为
		(3-69)
其中：1≤k≤K。 考虑U中任意给出的(N，M)，对于映射F有
		(3-70)
由于在式(3—69)，(3—70)中的映射F相同；同时从式(3—68)可知 故而必定有：
也即是有		(3-71)
或者		(3-72)

(2)对于图3-6所示的混合模糊神经网络，由于其输入是(N，M)；同时，(N，M) 属于紧集合U，而且必须至少是

集合中的元素之一，亦即N＝A_k，M＝B_k，1≤k≤K。令

G={k|λ_k=1,1≤k≤K}       (3-73)

由于λ_k不可能全部为0，故G是非空集。所以，有θ>0。
用m表示G所含的基本元素；为简单起见，设G＝{1，2，…，m}，则有

	(3-74)
	(3-75)
从而有
	(3-76)
(3)考虑距离d 可写成
	(3-77)
对于d(A，B)，如果β>0，A，B∈L。则有 同理，对于式(3—77)就有
	(3-78)
(4)对于L中的A，B，C，有
	(3-79)

首先，对于A，B，C的α截集有

这都是闭区间。故有

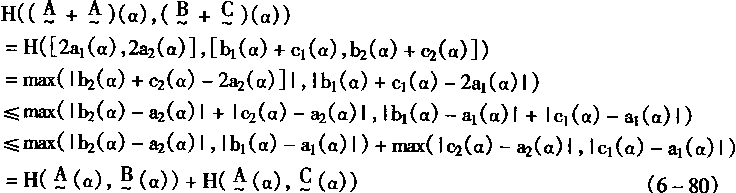
从式(3—59)，可知式(3—79)成立。

(5)最后考虑d(Q’，Q)

从式(3—76)．(3—77)，(3—78)可知

(3-81)

从中有

也可写成

故从式(3—79)，则有

	(3-82)
从式(3—72)，则有
	(3-83)

再从式(3—81)有

上一页         下一页