3.3 模糊神经网络的学习
在模糊神经网络中,混合模糊神经网络在目前还是表示一种算法,所以它不存在学习问题。所谓学习,是指对逻辑模糊神经网络和常规模彻神经网络而言的。在这一节中,分别介绍逻辑模糊神经网络的学习,算术模糊神经网络的学习方法。
3.3.1 逻辑模糊神经网络的学习算法
考虑图3—1所示的模糊神经元模型。在图中,xi,i=O,1,…,n,是模糊输入信号;Wj,j=0 ,1,…,n,是模糊权系数。
逻辑模糊神经网络的神经元模型是由式(3—3)来描述的。对于“或”神经元用式(3—4)(3-5)表示,而“与”神经元则用式(3—6)(3—7)表示。
设Yd是输出的期望值,Yd∈[-1,1]。而Y是模糊神经元的实际输出;则有输出误差e:
e-Yd-Y∈[-1,1]
执行学习的目的就是修改神经元中的权系数W'和增益参数g。使到输出的误差e最小。学习结构框图如图3—8所示。
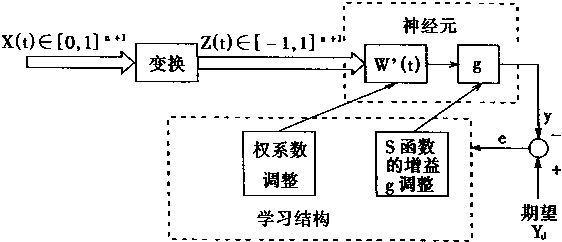
图3-8 模糊神经元学习框架
如果输入的信号属于[0,1]n+1超立方体空间的,则先变换到[-1,1]n+1超立方体空间。再送入神经元中,神经元的输出Y和给定的期望值Yd比较。产生误差e。学习机构根据误差的情况分别对权系数W和激发函数的增益g进行修改。使神经元的输出Y趋于期望Yd。
考虑神经元的输入和权系数向量分别如式(3—8),式(3—9)所示。
X(t)=[X0(t),X1(t),...,Xn(t)]T∈[0,1]n+1
W(t)=[W0(t),W1(t),...,Wn(t)]T∈[0,1]n+1
令
Zi(t)=2Xi(t)-1
Wi'(t)=2Wi(t)-1
则有
Z(t)=[Z0(t),Z1(t),...,Zn(t)]T∈[-1,1]n+1
W'(t)=[W0'(t),W1'(t),...,Wn'(t)]T∈[0,1]n+1
模糊神经元的学习算法如下
1.权系数W'的学习算法
W'(t+1)=W'(t)OR ΔW'(t)=S[W'(t),ΔW'(t)] (3-87)
其中
ΔW'(t)=Z(t) AND e(t)=T|Z(t),e(t)|
2.S函数的增益g的学习算法
g(t+1)=g(t) OR Δg(t)=S|g(t),Δg(t)| (3-88)
其中
Δg(t)=u(t) AND e(t)=T[u(t),e(t)]
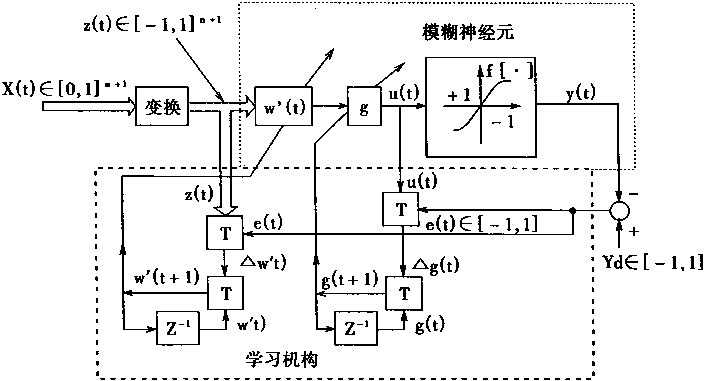
图3-9 模糊神经元的学习结构
在上面式(3—87)中,结出了模糊神经元权系数学习的算法;它也表示了一种模糊神经结构的实际模型。如果认为权系数是外部输人和树突输入之间的模糊关系,那么,模糊神经网络是可以通过经验进行学习的。
在上面式(3—88)中,修改g实际上是修改激发的灵敏度。因为参数g影响S函数的斜率,很明显也就影响神经元受激发的灵敏度。
模糊神经元的学习结构如图3—9中所示。
在图3—9中,很明显有2个学习环节,一个是权系数W'的学习环节,另一个是增益g的学习环节,它们是相互独立的。在这两个环节中,其中的Z-1处理框图是表示延时一个采样周期,故而它的输入为W'(t+1)时,输出为W'(t);输入为g(t+1)时,输出为g(t)。就是说这时Z-1的z是脉冲传递函数的符号;而不是双极信号z(t)中的信号。
3.3.2算术模糊神经网络的学习算法
算术模糊神经网络也称常规模糊神经网络,对算术模糊神经网络的学习算法随着这种网络的提出也同时提出了,但在这方面的研究方法有多种,而这些方法各有特点;在不同的场合和条件下有各自的优点。1992年,Buckley和Hayashi提出了模糊反向传播算法;同时.Ishibuchi等人提出了基于。截集的反向传播法。1994年,Buckley和Hayashi提出模糊神经网络的遗传算法。1995年,Ishibuchi等人提出了具有三角模糊权的模糊神经网络的学习算法。还有人提出了一些其它的算法。
在各种学习算法中,较有实际意义的是具有三角模糊权的模糊神经网络的学习算法.和遗传学习算法。
对于具有三角模物权的模城神经网络的学习算法,首先考虑模数数的模糊乘式(3—20)和模糊加式(3—23)。模糊非线性映射式(3—25),这些运算都是在水平截集的情况中执行的。
对于α截集,为了方便书写,这里不采用式(3—58)的表示方法,而采用下面表示方法:
对于模糊数N的α截集,用N[α]表示,并且有:
| (3-89) | |
| 其中:N(n)是隶属函数,R是全体实数集。 由于模糊数的水平截集是一个闭区间,故α截集N[α]可以表示为 |
|
| (3-90) | |
| 其中nL(α)是N[α]的下限值; nu(α)是N[α]的上限值。 根据区问算法,模糊数的运算可以写成α截集的运算 |
|
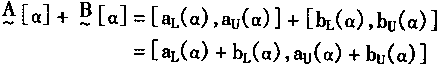 |
(3-91) |
![]()
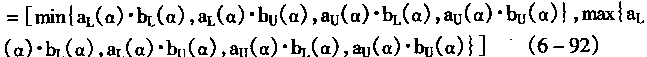
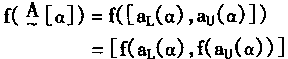 |
(3-93) |
| 在bu(α)>bL(α)>0的情况中,则式(3—92)可以简化为 | |
(3-94) | |
一、算术模糊神经网络输出的计算
考虑一个三层的前向神经网络,用I表示输入层,H表示隐层,O表示输出层。假设其输入、输出、权系数和阀值都是模糊量;其中输人、输出是任意模糊量,但权系数和阀值是三角模糊量。这种模糊神经网络如图3—10所示。
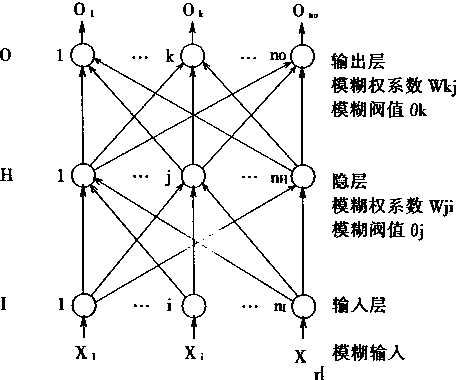
图3-10 模糊神经网络
很明显,对于图3—10所示的网络有如下输入输出关系,输人层的输出为Ii:
Ii=Xi
i=1,2,...,nI
(3-95)
隐层的输出为Hj:
Hj=f(Uj),j=1,2,...,nH (3-96)
| (3-97) | |
| 输出层的输出为Ok: Ok=f(Uk),k=1,2,...,nO |
(3-98) |
| (3-99) |
在上面(3—95)到(3—99)式中,Xi是模糊输入,Wji,Wkj是模糊权系数,θj,θk是模糊阀值。
为方便计算,在图3—10所示的模糊神经网络中,采用水平截集进行计算。对于α截集,则模糊神经网络输入输出关系可以写为下面式子:
对于输入层,有
Ii[α]=Xi[α] (3-100)
对于隐层,有
Hj[α]=f(Uj[α]) (3-101)
| (3-102) | |
| 对于输出层,有
Ok[α]=f(Uk[α]) (3-103) |
|
| (3-104) |
从上面(3—100)到(3—104)式中,可以看出:神经网络的模糊量α截集输出是由输入,隐层和阀值的α截集计算出来的。在输入的模糊量的α截集Xi[α]是非负的,即有
Xi[α]=[XL(α),XU(α)] (3-105)
并且
0≤XL(α)≤XU(α)
从而,对于输入层,隐层及输出层,可以用下列式子计算:
1.对于输入层:
Ii[α]=Xi[α]=[XiL(α),XiU(α)] (3-106)
2.对于隐层:
Hj[α]=[hjL(α),hjU(α)]
=[f(UjL(α)),f(UjU(α))]
(3-107)
其中
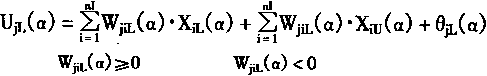 |
(3-108) |
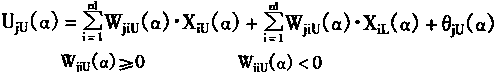 |
(3-109) |
3.对于输出层
Ok[α]=[OkL(α),OkU(α)]
=[f(UkL(α)),f(UkU(α))]
(3-110)
其中
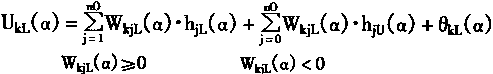 |
(3-111) |
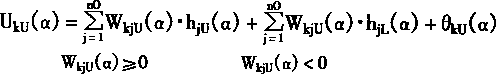 |
(3-112) |
二、模糊神经网络的学习
在模糊神经网络的学习中首先要给出目标函数,然后给出学习算法公式,再给出学习步骤。
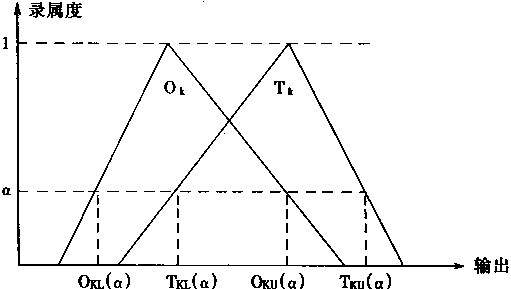
图3-11 目标函数
1.目标函数
考虑对应于模糊输人Xi, i=1,2,…,nI,有目标输出Tk, k=1,2,…,nO;对于网络的第k个输出端Ok的α截集以及相应的目标输出Tk,可以定义目标函数e。
在图3—11中,取Ok和Tk的α截集的上限值和下限值的误差的平方,并用 α值进行加权作为目标函数e,有
ek(α)=ekL(α)+ekU(α) (3-113)
其中:ekL( α)是Ok和Tk的 α截集的下限值的误差平方的。加权值:
| (3-114) | |
| ekU(α)是Ok和Tk的α截集的上限值的误差平方的 α加权值: | |
| (3-115) | |
| 从而Ok和Tk的α截集的目标函数可以定义为e( α) | |
| (3-116) | |
| 则输入输出对Xi,Tk的目标函数可以给出如下: | |
| (3-117) |
2.学习算法
假设三角模糊权系数Wkj,Wji可以用三个参数表示,即
Wkj=(WkjL,WkjC,WkjU) (3-118)
其中:WkjL是权系数的最小值,即其零截集的下限值;
WkjC是权系数的中值,即其顶角所对应的值;
WkjU是权系数的最大值,即其零截集的上限值;
Wji=(WjiL,WjiC,WjiU) (3-119)
其中参数的意义和Wkj中的类同。
很明显,有
| (3-120) | |
| (3-121) |
由于Wkj是表示隐层和输出层之间的权系数,可以先考虑其学习算法。根据梯度法.可以用目标函数对Wkj进行修正:
| (3-122) | |
| (3-123) |
其中: η是学习常数, β是修改常数。
在上面式(3-122),(3-123)中,说明利用目标函数e修改权系数的零截集下限值WkjL以及上限值WkjU;故而也就修改了权系数Wkj。
很明显,在式(3—122)(3—123)中,关键在于求取:
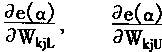
从e( α)的定义可知:e( α)必定是权系数Wkj的函数,故而也是Wkj的 α截集的上下限值的函数,即有
e( α)=g(WkjL( α),WkjU( α)) (3-124)
而WkjL,WkjU分别是Wkj的零截集的上下限值,则可知:
WkjL( α)是WkjL或WkjU的函数;WkjU( α)也是WkjL或WkjU的函数。
从全微分的角度则有:
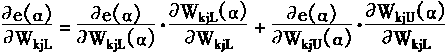 |
(3-125) |
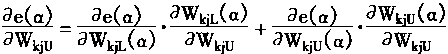 |
(3-126) |
为了求式(3—125)(3—126)的结果,很明显,需要求出WkjL、WkjU和WkjL( α)、WkjU( α)之间的关系。由于权系数Wkj是一个三角对称模糊数,它的形状如图3—12所示。
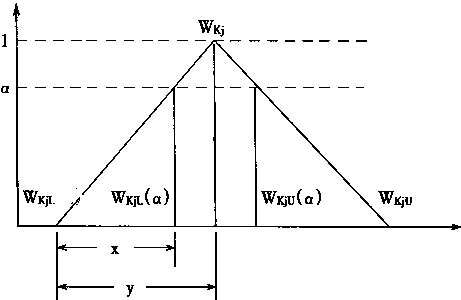
图3-12 WkjL、WkjU和WkjL( α)、WkjU( α)的关系示意
在图3-12中,可以看出有
![]()
即有 X=α.Y
实际上:![]()
故有
![]()
即
![]()
最后有
| (3-127) | |
| (3-128) | |
| 把式(3—127)(3—128)改写为下列形式 | |
| (3-129) | |
| (3-130) | |
| 上两式则明显说明WkjL、WkjU和WkjL(
α)、WkjU( α)的关系。 从而式(3—125)(3—126)则为: |
|
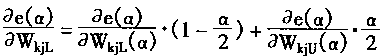 |
(3-131) |
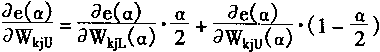 |
(3-132) |
很明显,要求取ae( α)/aWkjL,ae( α)/WkjU的结果,应首先求出ae( α)/aWkjL( α)和ae( α)/WkjU( α)的结果。由于从式(3—110)—(3—115)可知:e( α)、UkL( α)和WkjL( α)之间,e( α)、UkU( α)和WkjU( α)之间有一定的函数关系。故而有:
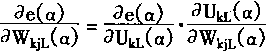 |
(3-133) |
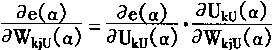 |
(3-134) |
考虑:
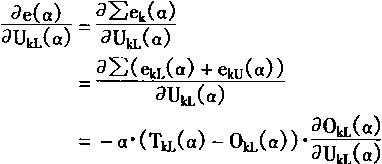
由于 OkL( α)=f(UkL( α))
而
![]()
故而
f'(X)=f(X).(1-f(X))
| (3-135) | |
| (3-136) |
对于aUkL( α)/aWkjL( α)和aUkU( α)/aWkjU( α),应考虑WkjL( α)和WkjU( α)的值不同的情况。
(1)当0 ≤WkjL( α) ≤WkjU( α)时
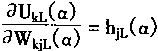 |
(3-137) |
| (3-138) | |
| (2)当WkjL( α) ≤WkjU( α) ≤0时 | |
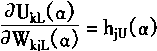 |
(3-139) |
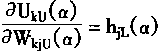 |
(3-140) |
| (3)当WkjL( α)<0 ≤WkjU( α)时 | |
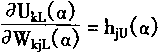 |
(3-141) |
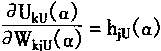 |
(3-142) |
很明显;从式(3—131)—(3—142)则能求出
![]()
的值,从而式(3—122)、(3—123)可解。
最后,对称三角形模糊权系数Wkj可以用下面公式进行学习校正
WkjL(t+1)=WkjL(t)+ ΔWkjL(t) (3-143)
WkjU(t+1)=WkjU(t)+ ΔWkjU(t) (3-144)
| (3-145) |
在校正之后.有可能出现WkjL>WkjU的情况,这时.令
WkjL(t+1)=min{WkjL(t+1),WkjU(t+1)}
WkjU(t+1)=max{WkjL(t+1),WkjU(t+1)}
对于模糊权系数Wji和模糊阀值 θj, θk.也可以采用模糊权系数Wkj的校正方法进行校正。
3.学习步骤
假设有m个模糊向量输入输出对(XP,TP),P=1,2,…,m;用于神经网络学习的截集有n个,即 α1, α2, α3,..., αn,在这种条件下,模糊神经网络的学习算法如下步骤:
(1)对模糊杖系数和模糊阀值取初值。
(2)对 α= α1, α2, α3,..., αn,重复执行第(3)步。
(3)对I=1,2,…’m;重复执行下列过程:
正向计算:对应于模糊输入向量Xp,求其输出模糊向量Op,并计算Op的。截集上下限。
反向传播:用目标函数e( α),校正神经网络的模糊权系数和模糊阀值。
(4)如果预定的结束条件未能满足,则返回第(2)步;否则校正结束。