3.3.3 模糊神经网络的遗传学习算法
在模糊神经网络中,也可以采用遗传学习算法对参数进行学习。在这一节中,用一个具体的例子说明遗传学习算法在模糊神经网络参数学习中的情况及其结果。
一、一些基本概念
在这一节中,假设所考虑的模糊量是实数模糊集。为了简单起见,这些实数模糊集表示为:A、B、……、W、V。模糊量A在x处的隶属度表示为A(x)。
模糊量A的α截集表示为:
A[α]={x|A(x)≥α},0<α≤1
下面给出三角模糊数的定义:
由3个数字a<b<c所定义的N称为三角模糊数,并且有如下性质:
1.当x≤a,或x≥c时,N(x)=0;
当x=b时,N(x)=1。
2.在[a,b]区间,从(a,0)到(b,1),y=N(x)是一条直线段;
在[b,c]区间,从(b,1)到(c,0),y=N(x)是一条直线段。
同理,可以给出三角形模糊数定义:
由3个数字a<b<c所定义的N称为三角形模糊数,并且有如下性质:
1.当x≤a,或x≥c时,N(x)=0;
当x=b时,N(x)=1。
2.在[a,b]区间,y=N(x)是一条单调增曲线;
在[b,c]区间,y=N(x)是一条单调减曲线。
无论是三角模糊数或三角形模糊数,都表示为:N=(a/b/c)。
如果a≥0,则称N≥0。
模糊数N的模糊测度表示为fuzz(N),并且有:
fuzz(N)=b—a
如果有fuzz(M)≥fuzz(N),则称M比N更模糊。
如果有M(x)≥N(x),对所有x,则表示为M≥N。
二、模糊神经网络结构
在这一节中,所给出的模糊神经网络是三层前向网络,它的输人,权系数都是模糊数。模糊神经网络的结构如图3—13中所示。
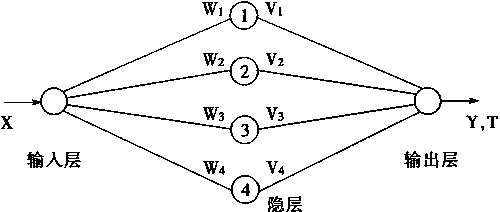
图3-13 模糊神经网络
在图3—13中,输入X.权系数w,v是三角模糊数,输出Y和目标T可以是三角形模糊数。
除了输入层之外,所有的神经元都有激发函数y=f(x),并且f是连续从R到[-t,t]的非单调减映射,t是正整数,R是实数域。
在隐层中,第i个神经元的输入为Ii,有:
Ii=X.Wi, 1≤i≤4 (3.146)
而第i个神经元的输出为Zi:
Zi=f(Ii), 1<i<4 (3.147)
在输出层,输出神经元的输入为I0
| (3.148) |
而在输出层产生的输出为Y
Y=f(I0) (3.149)
为了对模糊神经网络进行学习,所用的训练数据为
(X1,TI),1≤I≤L
其中:TI是在x1为输入时所需的输出。
学习中,实际输出为Y1, 1≤I≤L。
图3—13中所示的模糊神经网络的学习问题就是在输人为x1时,找寻最优的权系数Wi,Vi,使实际输出Yl逼近于T1,1≤1≤L。
三、模糊神经网络的遗传学习算法
遗传算法是一种直接随机搜索方法,它的主要步骤包括编码、选择、交叉、变异等。其原理在3.2节中已说明。在这里只对优化过程的目标函数及一些参数加以介绍。
1.模糊救
因3—13所示的模糊神经网络,优化的目的是找寻最优的权系数Wi、Vi:
Wi=(Wi1/Wi2/Wi3) (3.150)
Vi=(Vi1/Vi2/Vi3) (3.151)
其中:1≤i≤4
Wi2=(Wi1+Wi3)/2
Vi2=(Vi1+Vi3)/2
从上两式可知:只要知道Wi1、Wi3和Vi1、Vi3,就可以确定权系数Wi和Vi。因此,遗传算法只需对模糊权系数Wi、Vi的支持集进行追踪寻优即可。因此,群体的个体编码表示为P:
P=(W11,W13,......,V41,V43) (3.152)
P的编码采用二进制数。
2.遗传算法的有关参数
遗传算法的参数主要有3个,它们分别是群体数s,交叉车c,变异率M。一般是按经验进行选取。在这里,这些参数确定如下:
S=2000
C=0.8
M=0.0009
3.优化的目标函数
设Y1的α截集为Y1[α],有
Yl[α]=[yl1(α),yl2(α)] (3.153)
设Tl的α截集为Tl[α],有
Tl[]=[tl1(α),tl2(α)] (3.154)
α∈{0,0.1,0.1,......,0.9,1.0}
则定义
| (3.155) | |
| (3.156) |
E=E1+E2
遗传算法的目的就是寻找恰当的权系数Wi,Vi的值趋于0。
4.模糊神经网络的激发函数
图3—13所示的模糊神经网络中,隐层和输出层的激发函数f的意义如下:
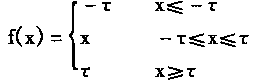 |
(3.157) |
其中:t是正整数,一般根据应用情况选择t的值。由于输出的目标模糊数T在[-1,1]区间之内,故在输出层中t的值通常取1。
四、学习情况
采用遗传算法对图3—13的模糊神经网络进行学习之后,可得出在不同输入输出要求下的学习结果。在这里给出一些具体的学习结果。
1.基本概念
(1)相同模糊度
如果对于输入X1和目标TI,存在:
fuzz(XI)=fuzz(TI), 1≤I≤L
则称输入和输出有相同模糊度,亦称等模糊。
(2)过模糊
如果对于输入X1和目标T1,存在:
fuzz(XI)<fuzz(TI), 1≤I≤L
则称输出为过模糊。
(3)欠模糊
如果对于输人X1和目标TI,存在
fuzz(XI)>fuzz(TI),1≤I≤L
则称输出为欠模糊。
2.等模糊的学习结果
训练数据用模糊函数F产生,故而有
T=F(X) (3.158)
由于是等模糊学习,故而必须选取函数F使
fuzz(T)=fuzz(X)
故而,选择如下式子
T=-X+1 (3.159)
从而,当X在[-1,1]区间时,则T处于[-2,2]区间。
给出训练数据如下表3—1所示。
表3-1 等模糊训练数据
|
编 号 |
输 入X |
输 出T |
| 1 | (-1/-0.75/-0.5) | (1.5/1.75/2) |
| 2 | (-0.25/0/0.25) | (0.75/1/1.25) |
| 3 | (0.5/0.75/1) | (0/0.25/0.5) |
在表3—1中,模糊数是三角或三角形模糊数,故用(a/b/c)方式表示。从表中看出:它们是对称三角模糊数。
在学习时,隐层和输出层的激发函数f都取式(3.157),不过由于输出层的目标T处于[-2,2],故t取值为2。在输出层f还加上一个需学习的偏置项,从而使神经网络可以学习-X+1,而得到T。在这种情况下,遗传学习取得很好的结果。并且,其权系数可以是实数。
3.过模糊的学习结果
训练数据采用如下公式产生:
T=A.X
其中:X在[-0.5,0.5]区间,
A=(1/1.5/2)
故而,目标T处于[-1,1]区间。
显然有:fuzz(T)>fuzz(X),即过模糊的结果。
训练数据给出如下表3—2所示。
表3-2 过模糊训练数据
| 编 号 | 输 入X | fuzz(X) | 输 出T | fuzz(T) |
| 1 | (-0.5/-0.25/0) | 0.5 | (-1/-0.375/0) | 1 |
| 2 | (-0.25/0/0.25) | 0.5 | (-0.5/0/0.5) | 1 |
| 3 | (0/0.25/0.5) | 0.5 | (0/0.375/1) | 1 |
在表3—2中,x是三角模糊数,T是三角形模糊数。
在隐层和输出层中,激发函数f中的t取值为1,所有的权系数都是模糊数。遗传算法 对训练数据执行很好的学习,并可使偏差E=0。
4.欠模糊的学习结果
训练数据由如下公式产生:
T=1/X
其中:X可在(-m,1)或[1,m]区间取值。故而T处于[-1,1]区间中。
显然有欠模糊结果:fuzz(T)<fuzz(X)。
为了训练,把X的值在[1,3]区间中选取,T是三角形模糊数。
训练数据给出如下表3—3所示。
表3-3 欠模糊训练数据
| 编 号 | 输 入X | fuzz(X) | 输 出T | fuzz(T) |
| 1 | (1/1.25/1.5) | 0.5 | 1/3 | |
| 2 | (1.5/1.75/2) | 0.5 | 1/6 | |
| 3 | (2/2.25/2.5) | 0.5 | 1/10 | |
| 4 | (2.5/2.75/3) | 0.5 | 1/15 |
在隐层中,激发函数f中的t取值为3。
模糊神经网络不能对这些训练数据进行学习。其主要原因在于式(3.157)所表示的激发函数是线性压缩函数,它无法满足对T=1/x这种非线性函数的逼近。如果f采用非线性压缩函数,则会较好进行学习。