回目录     上一页         下一页

第四章 神经模糊控制

用神经网络去实现模糊控制则称为神经模糊控制(Neuro-Fuzzy Control)。神经模糊控制是神经网络应用的一个重要方向。这种控制最吸引人的是能够对神经网络进行学习，从而可对模糊控制系统实现优化。

神经模糊控制有两种不同的实现方法。一种是用常规神经元和模糊神经元组成网络实现模糊控制；另一种是用模糊神经元组成网络实现控制。

模糊神经网络FNN3是典型的网络，Buckley等人证明了FNN3是一种单调映射，故而FNN3不是通用逼近器，但混合模糊神经网络HFNN则是通用逼近器。

模糊控制的控制曲面具有单调的特征，所以，模糊神经网络可以用于模糊控制。模糊控制中较多采用Mamdani以及Takagi-Sugeno推理。对于Mamdani推理，控制规则形式为：

Ri：if x is Ai and y is Bi then Z is Ci每条规则的击发强度为：

α_i=μ_Ai(X₀)Λμ_Bi(y₀)         (4.1)

其中：X0，Y0为输入。

则从控制规则中得到的控制为：

μ_c(z)＝V_i[α_iμ_ci(z)]         (4.2)

对于Takagi-Sugeno推理，控制规则的形式为：

Ri：if x is Ai and y is Bi then Z=fi(x,y)每条规则的击发强度为

α_i=μ_Ai(X₀)Λμ_Bi(y₀)

则从所有控制规则推得的结果为

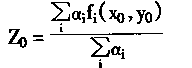(4.3)

很明显对于Mamdani推理，采用模糊神经元就可以建立模糊控制器；对于Takagi-Sugeno推理，则需要常规神经元和模糊神经元组成的网络来完成。故而．不同的推理方式对应的模糊神经网络有所不同。

4．1 神经模糊控制器

神经模糊控制器是用神经网络构成的模糊控制器；神经模糊控制器是神经模糊控制的核心。神经模糊控制器最关留的是结构和学习问题。

神经模糊控制器的结构应该是一种这样的拓扑结构，它可以处理模糊信息，并能完成模糊推理。

神经模糊控制器的学习则是一种能完成模糊推理的神经网络的学习。

在这一节中，介绍神经模糊控制器的结构及学习算法。

4．1．1 逻辑神经元组成的神经模糊控制器

逻辑神经元是模糊神经元的一种类型，用逻辑神经元可以构成执行Mamdani推理的模糊控制器。在这种模糊控制器中，每条控制规则可以用一个模糊神经网络实现。

一、模糊控制系统的参数

考虑一个模糊控制的过程，并且具有如下约定的参数：

在时间t时的输人为u(t)，输出为y(t)；设给定为s，则S也是输出的目标值。

设采样周期为T，并在离散时间t＝T，2T……时对输出进行检测。则偏差及偏差变化率求取如下：

e(t)=y(t)-s                  (4.4)

Δe(t)=[e(t)-e(t-T)]/T         (4.5)

对于模物控制器，其输入为e(t)，Δe(t)，模糊值输出为O(t)，反模糊化后的输出为U(t)。

模糊控制器的控制规则集为：

R_r：if e=A_i and Δe=B_i then O=C_p

1≤r≤g

在神经模糊控制器中，关键的是如何根据输入e、Δe而得到0，也即是实现模糊控制规则。

设A_i∈[a₁，b₁]，B_j∈[a₂，b₂]，C_p∈[a₃，b₃]，则在e、Δe和O的论域中，选取如下离散的点：

1．在[a1，b1]中取的离散点为X_i，并且有：

X_o=a₁                    (4.6)

X_i=a₁+i(b₁-a₁)/N₁        (4.7)

其中：1≤i≤N₁，N₁为正整数。

2.在[a₂，b₂]中取的离散点为y_i，并且有

y_o=a₂                  (4.8)

y_i=a₂+i(b₂-a₂)/N₂          (4.9)

其中：1≤i≤N₂，N₂为正整数。

3．在[a₃,b₃]中取的离散点为Z_i，并且有

Z_o=a₃                     (4.10)

Z_i=a₃+i(b₃-a₃)/N₃          (4.11)

其中：1<i<N₃，N₃为正整数。

对于给出的模糊控制规则中的模糊量A_i，B_j，C_p则有离散的隶属度：

A_i(x_j),0≤j≤N₁

B_j(y_k),0≤k≤N₂

C_p(Z_i),0≤i≤N₃

二、实现控制规则的神经网络

逻辑神经元组成的模糊神经网络如图4—1中所示。它有m个输入神经元，分别表示为I₁，I₂……I_m；同时有n个输出神经元，分别表示为Q₁，Q₂，…，Q_n。

设训练数据集为输入V_k和目标D_k，1≤k≤K，并且V_k和D_k都是向量：

V_k=(V_k1,V_k2,……,V_km)           (4.12)

D_k=(D_k1,D_k2,……,D_kn)           (4.13)

在给定输入为V_k时，有输出向量Q_k：

Q_k=(Q_k1,Q_k2,……,Q_kn)              (4.14)

在输入神经元I_j和输出神经元Q_i之间的权系数为r_ji，i＝1，2，……，n， j＝1，2，……，m。

在输出神经元Q_i中有偏置项θ_i，用θ表示θ_i向量，则有：

θ=(θ₁,θ₂,……,θ_n)          (4.15)

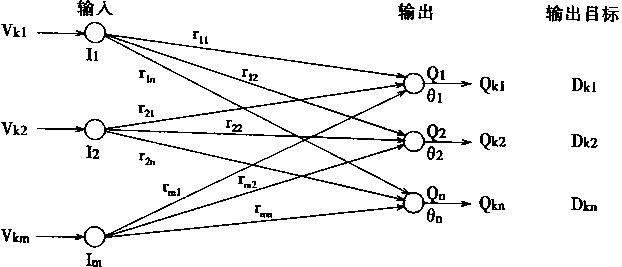
图4-1 模糊神经网络

在图4—1中，神经元是逻辑神经元，故而当给定输入V_k后，则有输出

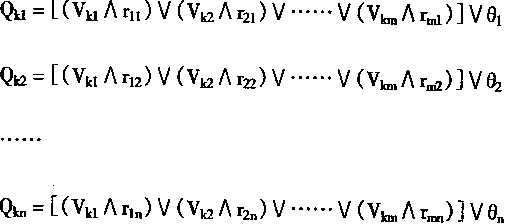
也可以用一个通式表示上面所有的n个式子

Q_ki=[(V_k1∧r_li)∨......∨(V_km∧r_mi)]∨θ_i            (4.16)

1≤i≤n

在图4—1中，把输入V_k看成是一个行向量，把偏置项θ看成—个行向量，并令

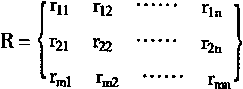(4.17)

则可以用向量方程描述神经网络的输入和输出如下

Q_k=(V_koR)∨θ                 (4.18)

对于模糊控制器而言，它可以是由控制规则集组成。对于控制规则集

R_r:if e=Ai and Δe=Bj then Q=C_p

1≤r≤g

则可以用一个神经网络模块实现一条规则，如果用n个神经网络模块则可以实现n条规则；也即是实现一个模糊控制器。

下面说明如何用一个神经网络模块实现一条控制规则。

在图4—1所示的神经网络可看成一个模块。根据式(4．6)(4．7)所表示的模糊量Ai所取的离散点有N₁+1个；式(4．8)(4．9)所表示的模糊量Bj所取的离散点有N₂+1个；式(4．10)(4．11)所表示的模糊量C_p所取的离散点有N₃+1个。令图4—1所示的神经网络模块中。

m=(N₁+1)+(N₂+1)=N₁+N₂+2                (4.19)

n=N₃+1                                 (4.20)

在输人的m个神经元中，把其中的N₁+1个神经元用于输入Ai；其中的N₂+1个神经元用于输入Bj。而输出的n个神经元用于目标C_p。并以此进行学习，则可以在学习结束时，得到能实现一条规则的一个神经网络模块。学习时，

A_i(X₀)——I₁

A_i(X₁)——I₂

……

A_i(X_N1)——I_N1+1

而同时

B_j(y₀)=I_N1+2

B_j(y₁)=I_N1+3

……

B_j(y_N2)=I_m

并且，输出目标为：

C_p(Z₀)——Q₁

C_p(Z₁)——Q₂

……

C_p(Z_N3)——Q_n

在控制规则集中，一共有g条规则，最后用g个神经网络模块，则可以实现模糊控制器。这个控制器即是神经模糊控制器。

4．1．2 神经模糊控制器的学习算法

图4—1所示的逻辑神经网络所组成的神经模糊控制器可以用改进的梯度法进行学习。

设给出的训练输人为Vk，目标为Dk，1≤k≤K，并且：

V_k=(V_k1,V_k2,…,V_km)

D_k=(D_k1,D_k2,…,D_kn)

而图4—1所示的网络在输入为V_k时，实际输出为Q_k。学习的目的，则是令Q_k逼近于D_k。实质上，就是修改网络的权系数r_ji，使到网络的插出Q_k趋于目标D_k。换而言之，也即是使式(4．18)中的Q_k＝D_k时，求其解R。即在

D_k=(V_koR)∨θ                     (4.21)

中，给出Dk，Vk，θ，求R。

为了进行学习，取目标函数J

	(4.22)
学习算法是采用改进的梯度算法，这个算法用下面两个公式表示
	(4.23)
	(4.24)

其中：l＝1，2，3，……是迭代次数

η_i，i＝1，2，是学习速率，

α_i，i＝1，2，是动量常数。

在式(4．23)(4．24)中，Δr_ji和Δθ_i的意义如下

	(4.25)
	(4.26)
对于Δrji，可计算如下
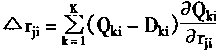	(4.27)
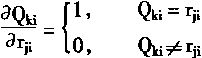	(4.28)

对于式(4．28)，可以解释如下：假定m＝2，n＝1，同时忽略下标k。则输入有V₁，V₂，对于V₁有权系数r₁，对于V₂有权系数r₂；两输出偏置项为θ。

设V₁＝0．7，V₂＝0．3，r₁＝1，r₂＝0．5，θ＝0．则根据式(4．18)有：

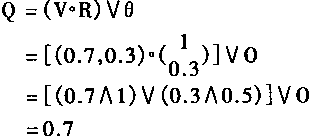
故而有

设V₁＝0．7，V₂＝0．3，r₁＝0.6，r₂＝0．5，θ＝0．则根据式(4．18)有：

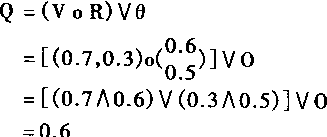
故而有

很明显，式(4．28)的意义是恰当的。

同样，对于Δθ_i，可计算如下：

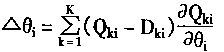	(4.29)
	(4.30)

为了保证r_ji(l+1)和θ_i(l+1)的值能处于[0，1]区间，故而给出附加的约束条件如下：

1．在式(4．23)中，如果式子右边得到的数值小于0，则令r_ji(l+1)＝0；如果式子右边得到的数值大于1，则令r_ji(l+1)＝1。

2．在式(4．24)中，如果式子右边得到的数值小于0，则令θ_i(l+1)＝0；如果式子右边得到的数值大于1，则令θ_i(l+1)＝1。

式(4.23)(4．24)所表示的学习算法对所选择的r_ji、的初值较为敏感。在初值选择时一般选θ_i=0。

4．1．3 多种神经元组成的神经模糊控制器

神经模糊控制器可以由多种神经元组成，这些神经元包括常规神经元，或神经元和与神经元等模糊神经元等。神经模糊控制器根据不同的推理规则，有不同的结构；所需的神经元不同，对于相同的推理规则其结构也不同。

一、Mamdani推理的模糊控制器
Mamdani推理规则的形式如下：
R_i：if x₁=A_i1 and x₂=A_i2 and ...... and x_n=A_in then y=B_j

当输入信号为精确值X0时有：

X₀＝{x₀₁，x₀₂，……，x_0n}

则对于前件，有隶属度：

A_i1(x₀₁)，A_i2(x₀₂)，……，A_in(x_0n)

对于第i条推理规则，则得到其前件的适合度W_i：

W_i=A_i1(x₀₁)∧A_i2(x₀₂)∧，……，∧A_in(x_0n) (4.31)

第i条推理规则的推理结果为

W_i∧B_i

全部规则在X₀作用时得到的推理结果为

B^*＝U_i(W_i∧B_i)                       (4.32)

根据Mamdani推理规则，用经向基函数RBF(Radial Basis Function)为激发函数的神经元，与神经元，或神经元，则可以组成模糊控制器。为了方便说明这种神经模糊控制器，考虑只在4条控制规则的情况。

对于模糊控制器来说，有2个输入x₁，x₂，1个输出y。

输人x₁的空间的模糊划分为“大”(L)，“小”(S)，并表示为A₁₁＝L，A₂₁＝S。

输入x₂的空间的模糊划分也为“大”(L)，“小”(S)，并表示为A₁₂＝L，A₂₂＝S。

输出y的空间的模糊划分为“大”(L)，“偏大”(ML)，“中”(M)，“小”(S)。

从而有4条推理规则：

if x₁=L and x₂=L then y=L

if x₁=L and x₂=S then y=ML

if x₁=S and x₂=L then y=M

if x₁=S and x₂=S then y=S

也可以写成：

if x₁=A₁₁ and x₂=A₁₂ then y=B₁

if x₁=A₁₁ and x₂=A₂₂ then y=B₂

if x₁=A₂₁ and x2=A₁₂ then y=B₃

if x₁=A₂₁ and x₂=A₂₂ then y=B₄

能完成这4条控制规则的神经模糊控制器如图4—2所示。

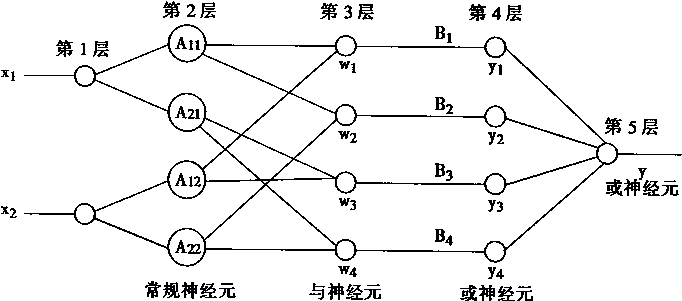
图4-2 Mamdani推理神经模糊控制器

当输入信号为x₁⁰，x₂⁰时，对第1—4条推理规则分别产生前件的适合度为W₁，W₂，W₃，W₄：

W₁=A₁₁(x₁⁰)∧A₁₂(x₂⁰)

W₂=A₁₁(x₁⁰)∧A₂₂(x₂⁰)

W₃=A₂₁(x₁⁰)∧A₁₂(x₂⁰)

W₄=A₂₁(x₁⁰)∧A₂₂(x₂⁰)

从而，对应的第1—4条规则所产生的推理结果分别是：

y₁=W₁∧B₁

y₂=W₂∧B₂

y₃=W₃∧B₃

y₄=W₄∧B₄

全部推理规则产生的最终结果为

	(4.33)
即有
	(4.34)

在图4—2中。所示的神经网络一共有5层，它们组成了一个模糊控制器．下面分别说明各层的意义和作用。

第1层：这是输入节点，只用于输入X1，X2的值。

第2层：这是模糊化层。这里的神经元是用径向基函数为激发函数的。径向基函数一般用高斯函数，钟形函数，梯形函数或三角形函数。径向基函数用于表述模糊量的隶属函数。

高斯函数(Gaussian function)的表达式如下：

G(x；a,c)=exp{-[(x-c)/a]²}               (4.35)

其中：c是函数的中心，

a是函数的宽度。

高斯函数的形状如图4—3所示。

钟形函数(Bell shape function)的表达式如下：

(4.36)

其中：c是函数的中心，

a是函数的宽度，

b是边缘的斜率参数。

钟形函数的形状如图4—4所示，在图中也给出了有关参数a，b，c的意义。

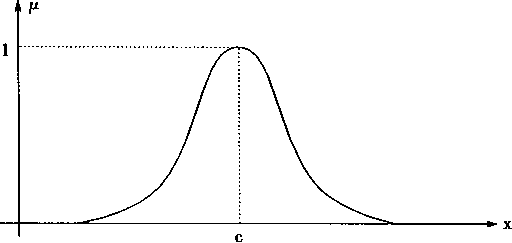
图4-3 高斯函数

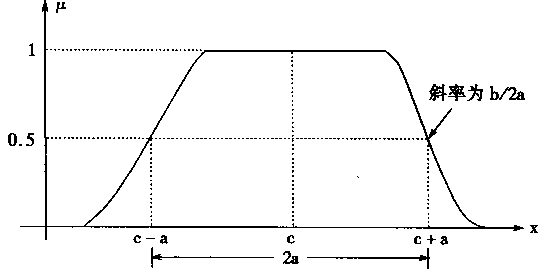
图4-4 钟形函数

梯形函数(Trapezoidal function)的表达式如下

	(4.37)
其中：a是梯形左边底角顶点坐标， b是梯形左边顶角顶点坐标， c是梯形右边顶角顶点坐标， d是梯形右边底角顶点坐标。 梯形函数的形状如图4—5所示。 三角形函数(Triangular function)的表达式如下
	(4.38)

其中：a是三角形左边底角顶点坐标，

b是三角形顶角顶点坐标，

c是三角形右边底顶角顶点坐标。

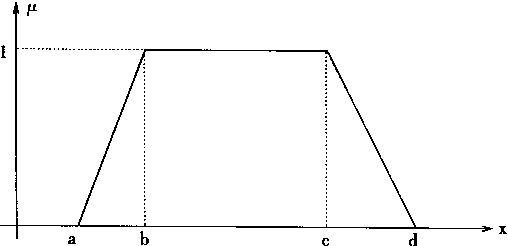
图4-5 梯形函数

三角形函数的形状如图4—6所示

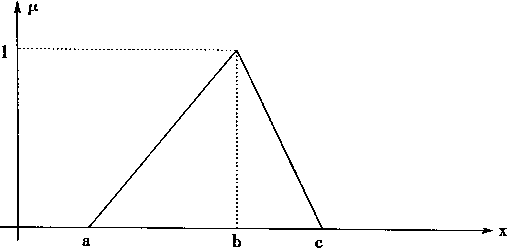
图4-6 三角形函数

显然，当在输入层有精确信号x输入，则在第2层就可以在径向基函数激发下产生对应的隶属度A(x)。
第3层完成控制规则的前件作用，它们是与神经元，用于产生每条规则的适合度。在图4—2中．第2层与第3层之间有连接，但没有权系数。显然有

W₁=A₁₁(x₁)∧A₁₂(x₂)

W₂=A₁₁(x₁)∧A₂₂(x₂)

W₃=A₂₁(x₁)∧A₁₂(x₂)

W₄=A₂₁(x₁)∧A₂₂(x₂)

第4层是或神经元，它用于完成控制规则后件的功能，产生每条规则对应于输入所产生的输出。第3层与第4层之间的连接权系数是控制规则的后件模糊量。故而有：

y₁=W₁∧B₁

y₂=W₂∧B₂

y₃=W₃∧B₃

y₄=W₄∧B₄

第5层是输出层，它用于产生控制规则的总输出。输出层是或神经元，在第4层和第5层之间的连接没有权系数。故而最后输出有：

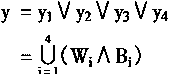
二、Takagi-Sugeno推理的神经模糊控制器

T—S推理的形式可以表示如下：

if x is A and y is B then Z=f(x,y)

为了方便说明问题，考虑如下4条具体的控制规则

if x=A₁ and y=B₁ then Z=a₁₀+a₁₁x+a₁₂y

if x=A₁ and y=B₂ then Z=a₂₀+a₂₁x+a₂₂y

if x=A₂ and y=B₁ then Z=a₃₀+a₃₁x+a₃₂y

if x=A₂ and y=B₂ then Z=a₄₀+a₄₁x+a₄₂y

根据这4条规则，对于前件，则有适合度

W₁=A₁(x)∧B₁(y)
W₂=A₂(x)∧B₂(y)
W₃=A₃(x)∧B₃(y)
W₄=A₄(x)∧B₄(y)

而在这4条规则的后件，则有输出

Z₁=a₁₀+a₁₁x+a₁₂y

Z₂=a₂₀+a₂₁x+a₂₂y

Z₃=a₃₀+a₃₁x+a₃₂y

Z₄=a₄₀+a₄₁x+a₄₂y

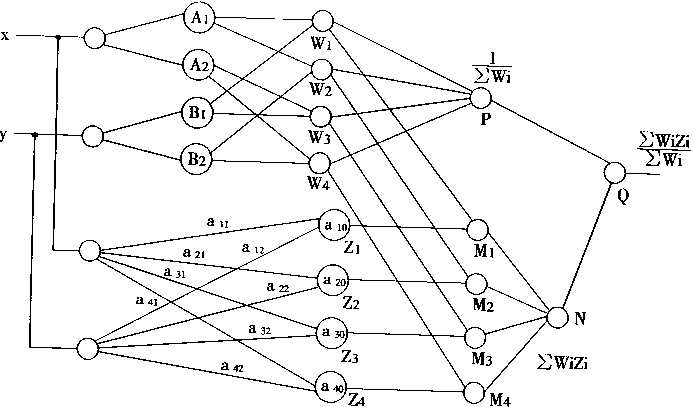
图4—7 Takagi-Sugeno推理神经模糊控制器

考虑这4条规则的总输出，则有

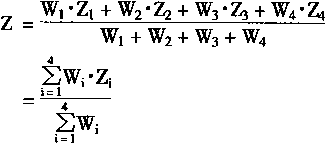
可以完成T—S推理的上述4条规则的神经网络如图4—7所示。在图4—7中的网络分成上下部分。上部分含有4层，下部分也有4层；上下两部分的输出再通过一个神经元Q产生最后的输出。

下面分别说明这个网络各部分的功能。

1．上部分网络

第1层：是输入层，它只是一个输入节点，并不是神经元。

第2层：是模糊化层。这层的神经元的激发函数采用高斯函数等径向基函数。在这一层可产生隶属度输出：A1(x)，A2(x)，B1(y)．B2(y)。

第3层：执行前件的功能，也就是求前件的适合度。这层采用与神经元；并且有

W₁=A₁(x)∧B₁(y)

W₂=A₁(x)∧B₂(y)

W₃=A₂(x)∧B₁(y)

W₄=A₂(x)∧B₂(y)

第4层；这层和第2层一样，也是常规神经元。第3层和第4层之间的连接没有权系数，并且．在第4层的神经元的激发函数为：

         f(x)=1/x

故而，有：

         p=1/∑W_i

2．下部分网络

第1层：和上部分网络一样，这一层只是输入节点。

第2层：它是常规神经元，并且在第1层和第2层之间存在连接权系数。权系数为a₁₁，

a₂₁，a₃₁，a₄₁，a₁₂，a₂₂，a₃₂，a₄₂。在这一层中，神经元的阀值为-a₁₀，-a₂₀，-a₃₀，-a₄₀。故而有输出：

Z₁=a₁₀+a₁₁x+a₁₂y

Z₂=a₂₀+a₂₁x+a₂₂y

Z₃=a₃₀+a₃₁x+a₃₂y

Z₄=a₄₀+a₄₁x+a₄₂y

第3层：用于求取每条规则输出的适合度，第3层和第2层之间的连接没有权系数；这里的第3层和上部分网络的第3层连接也没有权系数。并且，这一层的神经元是求积神经元。即有：

M₁=W₁Z₁         M₂=W₂Z₂

M₃=W₃Z₃         M₄=W₄Z₄

第4层：用于对策3层的输出求和。故它是一个常规神经元。这一层和第3层连接没有权系数。并且激发函数f(x)＝x。故有：

N=∑W_iZ_i

3．最终输出神经元Q

最终输出神经元Q是一个求积神经元。它的作用对输入信号求乘积。Q和P，N的连接没有权繁数。所以，Q的输出为

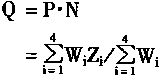
显然，图4—7完全可以实现上面所给出的执行T—S推理的4条规则的功能。也即是它是一个能完成T—S推理的神经模糊控制器。

上一页         下一页